Full-Length Accuplacer Math Practice Test-Answers and Explanations
Did you take the Accuplacer Math Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.
Accuplacer Mathematical Reasoning Practice Test Answers and Explanations
1- Choice A is correct
$7\(×\)8=$56, Petrol use: \(8×1.5=12\) liters
Petrol cost: 12\(×\)$1.5=$18. Money earned: $56\(-\)$18=$38
2- Choice D is correct
First, multiply the tenth place of 4.3 by 5.12. The result is 1.536. Next, multiply 4 by 5.12 which results in 20.48. The sum of these two numbers is: 1.536+20.48=22.016
3- Choice C is correct
Dividing 85 by \(25\%\), which is equivalent to 0.25, gives 340. Therefore, \(25\%\) of 340 is 85.
4- Choice A is correct.
\(\frac{15}{7}=2.14\), the only option that is greater than 2.14 is \(\frac{9}{4}\). \(\frac{9}{4}=2.25 ,2.25>2.14\)
5- Choice B is correct.
To compare fractions, find a common denominator. When two fractions have common denominators, the fraction with the larger numerator is the larger number. Choice A is incorrect because 4/5 is not less than 11/15. Write both fractions with a common denominator and compare the numerators. \(\frac{4}{5}=\frac{12}{15}\). The fraction \(\frac{12}{15}\) is greater than \(\frac{11}{15}\).
Choice C and D are not correct. Shown written with a common denominator, the comparisons \(\frac{4}{7}<\frac{7}{9}\) and \(\frac{4}{5}<\frac{16}{25}\) are not correct. Shown written with a common denominator, the comparison \(\frac{15}{21}<\frac{6}{7}\) is correct because \(\frac{6}{7}\) or \(\frac{18}{21}\) is greater than \(\frac{15}{21}\).
6- Choice D is correct.
Use this formula: Percent of Changefrac{New \ Value \ – \ Old \ Value}{Old Value}×100\%\)
\(\frac{24000-32000}{32000} ×100\%=25\% \) and \(\frac{8000-24000}{24000}×100\%=25\%\)
7- Choice B is correct
Let \(x\) be the original price. If the price of the sofa is decreased by \(13\%\) to $426.3, then: .\(87\%\) of \(x=426.3 ⇒ 0.87x=426.3 ⇒ x=426.3÷0.87=490\)
8- Choice B is correct
The percent of girls playing tennis is: \(30\% × 50\% = 0.30 × 0.50 = 0.15= 15\%\)
9- Choice C is correct
Write the equation and solve for B: 0.80 A = 0.40 B, divide both sides by 0.40, then:
0.80/0.40 A=B, therefore: B=2A and B is 2 times of A or it’s \(200\%\) of A.
10- Choice D is correct.
The closest to 7.025 is 7 in the options provided.
11- Choice C is correct.
Use distance formula: Distance = Rate \(×\) time ⇒ 390 = 60 \(×\) T, divide both sides by 60⇒390 / 60 = T ⇒ T = 6.5 hours. Change hours to minutes for the decimal part. 0.5 hours = 0.5 \(×\) 60 = 30 minutes.
12- Choice B is correct.
First simplify the multiplication: \(\frac{9}{4}×\frac{7}{3}=\frac{63}{12}=\frac{21}{4}=\frac{3×7}{4}\), Choice B is equal to \(\frac{6×7}{8}\)
\(\frac{6×7}{8}=\frac{3×7}{4}\)
13- Choice C is correct.
Use percent formula: part \(= \frac{percent}{100}×\) whole , \(84=\frac{percent}{100}×70 ⇒ 84=\frac{percent ×70}{100} ⇒\), multiply both sides by 100⇒ 8400=percent \(×\)70, divide both sides by 70. 120=percent
14- Choice A is correct.
To add decimal numbers, line them up and add from right. 1.78+3.045+2.007=6.832
15- Choice D is correct.
Use simple interest formula: I=prt (I=interest,p=principal,r=rte,t=time)
I=(15,000)(0.055)(6)=4,950
16- Choice B is correct.
87 divided by 7, the remainder is 3. 27 divided by 4, the remainder is also 3.
17- Choice D is correct.
\(\frac{18}{7}-\frac{11}{7}=\frac{7}{7}=1\)
18- Choice C is correct.
The question is this: 605.90 is what percent of 730? Use percent formula:
part\(=\frac{percent}{100}×\) whole, \(605.9=\frac{percent}{100}×730 ⇒ 605.9= \frac{percent ×730}{100} ⇒ 60590 =\) percent \(×730 ⇒\) percent \(=\frac{60590}{730}=83\)
605.9 is \(83\%\) of 730. Therefore, the discount is: \(100\% –83\%=17\%\)
19- Choice C is correct.
The weight of 9.5 meters of this rope is: \(9.5×380\) g=3,610
1 kg = 1,000 g, therefore, \(3,610 ÷1000=3.61\) kg
20- Choice B is correct.
Let’s compare each fraction: \(\frac{1}{3}<\frac{7}{11}< \frac{13}{19}<\frac{4}{5}\) Only choice B provides the right order.
The Absolute Best Book to Ace the Accuplacer Math Test
Answers and Explanations: Quantitative Reasoning, Algebra, And Statistics
21- Choice B is correct.
Use Pythagorean Theorem: \(a^2+b^2=c^2, 8^2 + 15^2 = c^2 ⇒ 64+225=c^2 ⇒ 289=c^2⇒c=17\)
22- Choice C is correct.
The sum of supplement angles is 180. Let \(x\) be that angle. Therefore, \(x = \frac{2}{9}×180, x = 40\)
23- Choice B is correct.
The average speed of john is: 210÷7=30 km
The average speed of Alice is: 175÷5=35 km
Write the ratio and simplify. 30: 35 ⇒ 6: 7
24- Choice A is correct.
\($8.5×10=$85\), Petrol use: \(10×3=30\) liters, Petrol cost: \(30×$1.5=$45\)
Money earned: \($85-$45=$40\)
25- Choice D is correct.
Let \(x\) be the number. Write the equation and solve for \(x. (45 – x) ÷ x = 4\)
Multiply both sides by \(x. (45 – x) = 4x\), then add \(x\) both sides. \(45 = 5x\), now divide both sides by 5. \(x = 9\)
26- Choice B is correct.
The equation of a line is in the form of \(y=mx+b\), where m is the slope of the line and b is the y-intercept of the line. Two points \((-3,2)\) and \((2,-8)\) are on line A. Therefore, the slope of the line A is: slope of line A \(=\frac{y_2- y_1}{x_2 – x_1} = \frac{-8-2}{2-(-3)}=\frac{-10}{5}=-2\)
The slope of line A is \(-2\). Thus, the formula of the line A is: \(y=mx+b=-2x+b\), choose a point and plug in the values of \(x\) and \(y\) in the equation to solve for b. Let’s choose point \((-3,2)\). Then: \(y=-2x+b→2=-2(-3)+b→b=2-6=-4\), The equation of line A is: \(y=-2x-4\), Now, let’s review the choices provided:
A. \((-1,3) y=-2(-1)-4→3=2-4=-2\) This is not true.
B. \((-2,0) y=-2(-2)-4→0=4-4=0\) This is true!
C. \((3,4) y=-2(3)-4→4=-6-4=-10\) This is not true.
D. \((-1,-5) y=-2(-1)-4→-5=2-4=-2\) This is not true
27- Choice C is correct.
If the length of the box is 40, then the width of the box is one-fourth of it, 10, and the height of the box is 5 (one second of the width). The volume of the box is: \(V = lwh\) \(=\) (40) (10) (5) = 2000
28- Choice D is correct.
To find the number of possible outfit combinations, multiply the number of options for each factor: \(4×5×7=140\)
29- Choice A is correct.
The area of the trapezoid is: Area \(=\frac{1}{2} h(b_1+b_2 )=\frac{1}{2}(x)(24+16)=300→20x=300→x=15⇒ y=\sqrt{8^2+15^2 }=\sqrt{64+225}=\sqrt{289}=17\)
The perimeter of the trapezoid is: 16+8+17+16+15=72
30- Choice A is correct.
The area of the circle is less than 121 π. Use the formula of areas of circles.
Area \(= πr^2 ⇒ 121 π> πr^2⇒ 121 > r^2⇒ r < 11\)
The radius of the circle is less than 11. Let’s put 11 for the radius. Now, use the circumference formula: Circumference =2πr=2π (11)=22 π
Since the radius of the circle is less than 11. Then, the circumference of the circle must be less than 22 π. Only choice A is less than 22 π.
31- Choice D is correct.
There are 25 integers from 5 to 30. Set of numbers that are not composite between 5 and 30 is: { 5,7,11,13,17,19,23,29}⇒ 8 integers are not composite. Probability of not selecting a composite number is: Probability \(= \frac{number \ of \ desired \ outcomes}{number \ of \ total \ outcomes}=\frac{ 8}{25}\)
32- Choice C is correct.
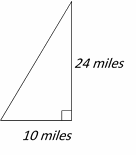
Use the information provided in the question to draw the shape.
Use Pythagorean Theorem: \(a^2+ b^2=c^2 , 24^2+ 10^2=c^2
⇒ 576+100= c^2 ⇒ 676=c^2 ⇒ c=26\)
33- Choice C is correct.
The ratio of boys to girls is 2:5. Therefore, there are 2 boys out of 7 students. To find the answer, first, divide the total number of students by 7, then multiply the result by 2.
\(56÷7=8 ⇒ 8×2=16\) There are 16 boys and \(40 (56 – 16) \) girls. So, 24 more boys should be enrolled to make the ratio 1:1
34- Choice C is correct.
If the score of Mia was 72, therefore the score of Ava is 36. Since the score of Emma was two-thirds of that of Ava, therefore, the score of Emma is 24.
35- Choice A is correct.
Let \(x\) be the number. Write the equation and solve for \(x\).
\(\frac{3}{7} ×21= \frac{3}{5} . x ⇒ (\frac{3×21}{7}= \frac{3x}{5}\) , use cross multiplication to solve for \(x\).
\(5×63=3x×7 ⇒315=21x ⇒ x=15\)
36- Choice C is correct.
Let \(x\) be the number of years. Therefore, $1,200 per year equals \(1200x\). Starting from a $15,000 annual salary means you should add that amount to \(1200x\).
Income more than that is: \(I>1200x+15000\)
37- Choice D is correct.
average \(=\frac{sum \ of \ terms}{number \ of \ terms}\), The sum of the weight of all girls is: 15×50=750 kg
The sum of the weight of all boys is: 25×60=1500 kg
The sum of the weight of all students is: 750+1500=2250 kg, average \(=\frac{2250}{40}=56.25\)
38- Choice D is correct.
Write the numbers in order: 6,10,13,15,18,21,25
Since we have 7 numbers (7 is odd), then the median is the number in the middle, which is 15.
39- Choice A is correct.
Formula for the Surface area of a cylinder is: \(SA=2πr^2+2πrh→48π=2πr^2+2πr(5)→r^2+5r-24=0 ⇒ (r+8)(r-3)=0→r=3 or r= -8\) (unacceptable)
40- Choice B is correct.
Let \(x\) be the smallest number. Then, these are the numbers: \(x, x+1, x+2, x+3, x+4, x+5\). Average \(= \frac{sum \ of \ terms }{number \ of \ terms} ⇒ 67.5=\frac{x+(x+1)+(x+2)+(x+3)+(x+4)+(x+5)}{6}⇒67.5=\frac{6x+15}{6} ⇒ 405=6x+15 ⇒ 390=6x ⇒ x=65\)
Best Accuplacer Math Prep Resource for 2024
Answers and Explanations: Advanced Algebra and Functions
41- Choice D is correct
You can find the possible values of and b in \((ax+3)(bx-4)\) by using the given equation \(a+b=5\) and finding another equation that relates the variables a and b. Since \((ax+3)(bx-4)=-6x^2+2cx+10\), expand the left side of the equation to obtain
\(abx^2-4ax+3bx-12=-6x^2+2cx+10\)
Since \(ab\) is the coefficient of \(x^2\) on the left side of the equation and 10 is the coefficient of \(x^2\) on the right side of the equation, it must be true that \(ab=-6\)
The coefficient of \(x\) on the left side is \(3b-4a\) and the coefficient of \(x\) in the right side is \(2c\). Then: \(\frac{3b-4a }{2}=c, a+b=5\), then: \(a=5-b\)
Now, plug in the value of a in the equation \(ab=-6\). Then: \(ab=-6→(5-b)b=-6→5b-b^2=-6⇒\) Add \(-5b+b^2\) both sides. Then: \(b^2-5b-6=0\)
Solve for b using the factoring method. \(b^2-5b-6=0→(b-6)(b+1)=0\)
Thus, either \(b=6\) and \(a =-1\), or \(b =-1\) and \(a =6\). If \(b =6\) and \(a =-1\), then:
\(c=\frac{3b-4a}{2}=\frac{3(6)-4(-1) }{2}=11\). If \(b=-1\) and \(a =6\), then, \(c=\frac{3b-4a }{2}=\frac{3(-1)-4(6) }{2}=\frac{27}{2}=13.5→c=13.5\). Therefore, the two possible values for c are 11 and 13.5.
Method 2: Multiplying each side of \(3x+2y=0\) by \((-1)\) gives \(-3x-2y=0\). Then, adding the corresponding side of \(-3x-2y=0\) and \(3x-4y=6\) gives \(-6y=6\). Dividing each side of \(-6y=6\) by \((-6)\) gives \(y=-1\). Finally, substituting \((-1)\) or \(y\) in \(3x+2y=0\), or \(y=\frac{2}{3}\). Therefore, the solution to the given system of equations is \((\frac{2}{3},-1)\).
42- Choice C is correct
If \(f(x)=7x+2(1-x)\), then find \(f(3x)\) by substituting \(3x\) for every \(x\) in the function. This gives: \(f(3x)=7(3x)+2(1-(3x)) ⇒\) It simplifies to: \(f(3x)=7(3x)+2(1-(3x))=21x+2-6x=15x+2\)
43- Choice D is correct
First, find the equation of the line. All lines through the origin are of the form \(y=mx\), so the equation is \(y=\frac{2}{5} x\). Of the given choices, only choice D (15,6), satisfies this equation:
\(y=\frac{2}{5} x→6=\frac{2}{5} (15)=6\)
44- Choice B is correct
\((4n^2-5n+12)-(3n^2-4n)\). Add like terms together: \(4n^2-3n^2=n^2
-5n+4n=-n\). 12 doesn’t have like terms
Combine these terms into one expression to find the answer: \(n^2-n+12\)
45- Choice A is correct
Method 1: Plugin the values of x and y provided in the options into both equations.
A. \((\frac{2}{3},-1) 3x+2y=0→3(2/3)+2(-1)=0\)
B. \((5,- 4) 3x+2y=0→3(5)+2(-4)≠0\)
C. \((4,-4) 3x+2y=0→3(4)+2(-4)≠0\)
D. \((\frac{5}{3},-6) 3x+2y=0→3(5/3)+2(-6)≠0\)
Only option A is correct.
46- Choice A is correct
To solve this problem, first recall the equation of a line: \(y=mx+b\)
Where m=slope. \(y=y-\)intercpt
Remember that slope is the rate of change that occurs in a function and that the \(y\)-intercept is the \(y\) value corresponding to \(x=0\).
Since the height of John’s plant is 8 inches tall when he gets it. Time (or \(x\)) is zero. The plant grows 5 inches per year. Therefore, the rate of change of the plant’s height is 5. The \(y\)-intercept represents the starting height of the plant which is 5 inches.
47- Choice A is correct
Since (1, 2) is a solution to the system of inequalities, substituting 1 for \(x\) and 2 for \(y\) in the given system must result in two true inequalities. After this substitution, \(y>-a-x\) becomes \(-3 < a\), and \(y > x+b\)becomes \(1 > b\). Hence, a is more than -3 and b is less than 1.
Therefore, \(b>a\).
48- Choice C is correct
First find the slope of the line using the slope formula. \(m=\frac{y_2-y_1}{x_2-x_1 }\)
Substituting in the known information. \((x_1, y_1 )=(1,-5), (x_2, y_2 )= (-3,7)
m=\frac{7-(-5)}{-3-1}=-\frac{12}{4}=-3\)
Now the slope to find the equation of the line passing through these points. \(y=mx+b\)
Choose one of the points and plug in the values of \(x\) and \(y\) in the equation to solve for b.
Let’s choose point \((1,-5)\). Then: \(y=mx+b→-5=-3(1)+b→-5=-3+b→b=-5+3=-2\), The equation of the line is: \(y=-3x-2\)
Now, plug in the points provided in the choices into the equation of the line.
A. \((2,-3) \ \ \ y=-3(2)-2=-8\) This is NOT true.
B. \((5,-12) \ \ \ y=-3(5)-2=-17\) This is NOT true.
C. \((-4,10) \ \ \ y=-3(-4)-2=10\) This is true.
D. \((3,- 6) \ \ \ y=-3(3)-2=-11\) This is NOT true!
Therefore, the only point from the choices that lie on the line is \((-4,10)\).
49- Choice B is correct
The input value is 5. Then: \(x=-4⇒ f(x)=2x^2+4x+1→f(-4)=2(-4)^2+4(-4)+1=17\)
50- Choice B is correct
To rewrite \(\frac{1}{\frac{1}{x+4}+\frac{1}{x-9}}\), first simplify \(\frac{1}{x+4}+\frac{1}{x-9}\).
\(\frac{1}{x+4}+\frac{1}{x-9}=\frac{1(x-9)}{(x-9)(x+4)}+\frac{1(x+4)}{(x+4)(x-9)}=\frac{(x+4)+(x-9)}{(x+4)(x-9)}\)
Then: \(\frac{1}{\frac{1}{x-9}+\frac{}{x+4}}=\frac{1}{\frac{(x+4)+(x-9)}{(x+4)(x-9)}}=\frac{(x-9)(x+4)}{(x+4)+(x-9)}\). (Remember, \(\frac{1}{\frac{1}{x}}=x)\)
This result is equivalent to the expression in choice B.
51- Choice B is correct
The line passes through the origin, (2,m) and (m,10).
Any two of these points can be used to find the slope of the line. Since the line passes through (0, 0) and (2,m), the slope of the line is equal to \(\frac{m-0}{2-0}=\frac{m}{2}\). Similarly, since the line passes through (0, 0) and (m,10), the slope of the line is equal to \(\frac{10-0}{m-0}=\frac{10}{m}\). Since each expression gives the slope of the same line, it must be true that \(\frac{m}{2}=\frac{10}{m}\)
Using cross multiplication gives , \(\frac{m}{2}=\frac{10}{m}→m^2=20 →m=±\sqrt{20}=±\sqrt{4×5}=±\sqrt{4}×\sqrt{5}=±2\sqrt{5}\)
52- Choice A is correct
The equation of a circle can be written as \((x-h)^2+(y-k)^2=r^2\)
where (h,k) are the coordinates of the center of the circle and r is the radius of the circle. Since the coordinates of the center of the circle are \((1,-2)\), the equation is \((x-1)^2+(y+2)^2=r^2\), where r is the radius. The radius of the circle is the distance from the center \((1,-2)\), to the given endpoint of a radius, \((\frac{1}{3},2)\). By the distance formula, \(r^2=(\frac{1}{3}-1)^2+(2+2)^2=\frac{148}{9}\), Therefore, an equation of the given circle is \((x-1)^2+(y+2)^2=\frac{148}{9}\)
53- Choice C is correct
To solve for cos A first identify what is known.
The question states that ∆ABC is a right triangle whose \(n∠B=90^\circ\) and sin C \(=\frac{3}{5}\).
It is important to recall that any triangle has a sum of interior angles that equals 180 degrees. Therefore, to calculate cos A use the complementary angles identify of the trigonometric function. cos A=cos \((90-\)C), Then: cos A=sinC
For complementary angles, the sin of one angle is equal to the \(cos\) of the other angle. cos A \(=\frac{3}{5}\)
54- Choice D is correct
To figure out what the equation of the graph is, first find the vertex. From the graph, we can determine that the vertex is at \((2,-3)\).
We can use vertex form to solve the equation of this graph.
Recall vertex form, \(y=a (x-h)^2+k\), where \(h\) is the \(x\) coordinate of the vertex, and k is the \(y\) coordinate of the vertex. Plugging in our values, you get \(y=a(x-2)^2-3\)
To solve for a, we need to pick a point on the graph and plug it into the equation.
Let’s pick \((4,1), 1=a(4-2)^2-3, 1=a(2)^2-3, 1=4a-3, a=1⇒\) Now the equation is : \(y=(x-2)^2-3\), Let’s expand this, \(y=(x^2-4x+4)-3, y=x^2-4x+1\)
\(y=x^2-4x+1\). The equation in Choice D is the same.
55- Choice B is correct
Multiplying each side of \(\frac{7}{x}=\frac{21}{x+4}\) by \(x(x+4)\) gives \(7(x+4)=21x\),divide two side by 7.
\(x+4=3x or x=2\). Therefore, the value of \(-\frac{x}{3}=-\frac{2}{3}\).
56- Choice D is correct
It is given that \(g(6)=8\). Therefore, to find the value of \(f(g(6))\), then \(f(g(6))=f(8)=12\)
57- Choice C is correct
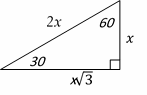
The area of the triangle is: \(\frac{1}{2}\) AD×BC and AD is perpendicular to BC. Triangle ADC is a \(30^\circ-60^\circ- 90^\circ\) right triangle. The relationship among all sides of the right triangle \(30^\circ-60^\circ- 90^\circ\) is provided in the following triangle: In this triangle, the opposite side of \(30^\circ\) angle is half of the hypotenuse. And the opposite side of \(60^\circ\) is opposite of \(30^\circ × \sqrt{3}\)
CD = 7, then AD \(= 7 × \sqrt{3}\)
Area of the triangle ABC is: \(\frac{1}{2}\) AD×BC = \(\frac{1}{2} 7\sqrt{3}×14=49\sqrt{3}\)
58- Choice D is correct
It is given that \(g(4)=10\). Therefore, to find the value of \(f(g(4))\), substitute 10 for \(g(4)\).
\(f(g(4))=f(10)=40\).
59. Choice A is correct
The equation of a circle with center (h, k) and radius r is \((x-h)^2+(y-k)^2=r^2\). To put the equation \(x^2+y^2-6x+4y=4\) in this form, complete the square as follows:
\(x^2+y^2-6x+4y=4, (x^2-6x)+(y^2+4y)=4\)
\((x〗^2-6x+9)-9+(y^2+4y+4)-4=4, (x-6)^2+(y+4)^2=17\)
Therefore, the radius of the circle is \(\sqrt{17}\)
60- Choice A is correct
By definition, the tan of any acute angle is equal to the \(cot\) of its complement.
Since angles A and B are complementary angles, therefore:
tan A=cot B
The Best Books to Ace the Accuplacer Math Test
Related to This Article
More math articles
- Full-Length 6th Grade MCAS Math Practice Test-Answers and Explanations
- TASC Testing Accommodation and Support for Disabilities
- Getting Better at Math: Realistic Tips and Suggestions
- FREE 7th Grade MEAP Math Practice Test
- The Ultimate 7th Grade Scantron Math Course (+FREE Worksheets)
- 10 Most Common 5th Grade OST Math Questions
- How to Divide by Zero?
- What Is the Highest Score for SHSAT Test?
- Matching a Model with a Ratio
- FREE 7th Grade STAAR Math Practice Test
What people say about "Full-Length Accuplacer Math Practice Test-Answers and Explanations - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.