FREE PSAT Math Practice Test

The Absolute Best Book to Ace the PSAT Math Test

10 Sample PSAT Math Practice Questions

1-

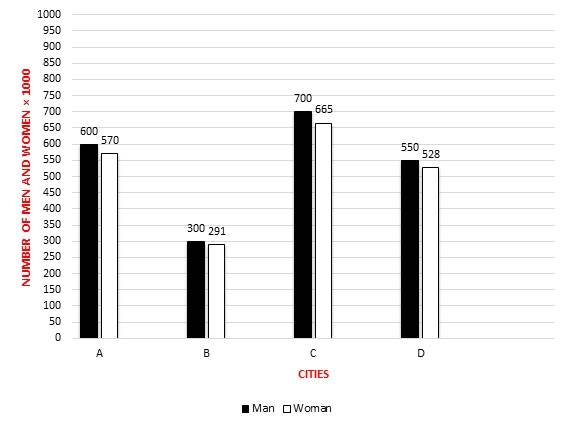
Based on the graph, how many women should be added to city D until the ratio of women to men will be 1.2?

A. 120

B. 128

C. 132

D. 160

2- In the rectangle below if \(y>5\) cm and the area of a rectangle is 50 square centimeters and the perimeter of the rectangle is 30 cm, what is the value of \(x\) and \(y\) respectively?

A. 4, 11

B. 5, 11

C. 5, 10

D. 4, 10

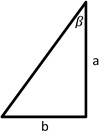
3- Given the right triangle ABC bellow, sin⁡(\(β\)) is equal to?

A. \(\frac{a}{b}\)

B. \(\frac{a}{\sqrt {(a^2+b^2 )}}\)

C. \(\frac{\sqrt {(a^2+b^2 )}}{ab}\)

D. \(\frac{b}{\sqrt{(a^2+b^2 )}}\)

4- Solve the following inequality.
\(|\frac{x}{2}-2x+10|<5\)

A. \(-\frac{10}{3}< x < 10\)

B. \(-10 < x <\frac{10}{3}\)

C. \(\frac{10}{3} < x < 10\)

D. \(-10 < x < -\frac{10}{3}\)

5- \(f(x)= ax^2+bx+c\) is a quadratic function where a, b and c are constant. The value of x of the point of intersection of this quadratic function and the linear function \(g(x) = 2x – 3\) is 2. The vertex of \(f(x)\) is at (-2, 5). What is the product of a, b, and c? ___________

6- A ladder leans against a wall forming a \(60^\circ\) angle between the ground and the ladder. If the bottom of the ladder is 30 feet away from the wall, how many feet is the ladder? __________

7- The volume of cube A is \(\frac{1}{2}\) of its surface area. What is the length of an edge of cube A? ____________

8- If \(3x + 6y = \frac{-3y^2+15}{x}\) , what is the value of \((x+y)^2\) \((x≠0)\)?

9- If \(3x – 5 = 8.5\), what is the value of \(5x + 3\) ?

A. 13

B. 15.5

C. 20.5

D. 25.5

10- In a certain bookshelf of a library, there are 35 biology books, 95 history books, and 80 language books. What is the ratio of the number of biology books to the total number of books in this bookshelf?

A. \(\frac{1}{4}\)

B. \(\frac{1}{6}\)

C. \(\frac{2}{7}\)

D. \(\frac{3}{8}\)

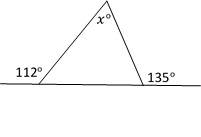
11- In the figure below, what is the value of \(x\)?

A. 43

B. 67

C. 77

D. 90

12- The following table represents the value of \(x\) and function \(f(x)\). Which of the following could be the equation of the function \(f(x)\)?

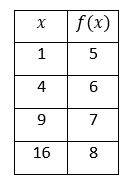
A. \( f(x)=x^2-5\)

B. \( f(x)=x^2-1\)

C. \(f(x)=\sqrt{(x+2)}\)

D. \(f(x)=\sqrt x+4 \)

13- If \(xp + 2yq = 26\) and \(xp + yq = 17\), what is the value of \(yq\)?

A. 6

B. 7

C. 8

D. 9

14- The circle graph below shows all Mr. Green’s expenses for last month. If he spent $660 on his car, how much did he spend for his rent?

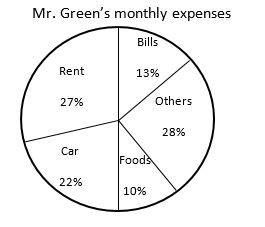
A. $700

B. $740

C. $780

D. $810

15- If \(x^2+3\) and \(x^2-3\) are two factors of the polynomial \(12x^4+n\) and n is a constant, what is the value of n?

A. \(-108\)

B. \(-24\)

C. 24

D. 108

16- The letters represent two decimals listed above. One of the decimals is equivalent to \(\frac{1}{8}\) and the other is equivalent to \(\frac{1}{20}\). What is the product of C and D?

A. 0

B. 5

C. 25

D. 20

17- The radius of circle A is three times the radius of circle B. If the circumference of circle A is \(18π\), what is the area of circle B?

A. \(3π\)

B. \(6π\)

C. \(9π\)

D. \(12π\)

18- If the function\( ƒ\) is defined by \(f(x)=x^2+2x-5\), which of the following is equivalent to \(f(3t^2)\)?

A. \( 3t^4+6t^2-5\)

B. \( 9t^4+6t^2-5\)

C. \( 3t^4+3t^2-5\)

D. \( 3t^4+6t^2+5\)

19- In the diagram below, circle A represents the set of all odd numbers, circle B represents the set of all negative numbers, and circle C represents the set of all multiples of 5. Which number could be replaced with \(y\)?

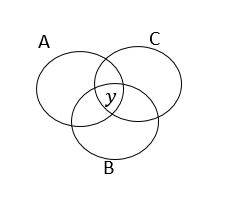
A. 5

B. 0

C. \(-5\)

D. \(-10\)

20- There are only red and blue marbles in a box. The probability of choosing a red marble in the box at random is one fourth. If there are 132 blue marbles, how many marbles are in the box?

A. 140

B. 156

C. 176

D. 190

Best PSAT Math Prep Resource for 2024

Answers:

2- C
The perimeter of the rectangle is:
\(2x + 2y = 30 → x + y =15→ x = 15 – y\)
The area of the rectangle is:
\(x × y = 50 → (15 – y)(y) = 50→ y^2 – 15y + 50 = 0\)
Solve the quadratic equation by factoring method.
\((y – 5)(y – 10) = 0→y = 5\)
(Unacceptable, because y must be greater than 5) or \(y = 10\)
If \(\space y = 10 →x × y = 50→x × 10 = 50→x = 5\)

3- D
sin⁡\(β = \frac{opposit \space side}{hypotenuse}\)
To find the hypotenuse, we need to use the Pythagorean theorem.
\(a^2+b^2=c^2→c=\sqrt{(a^2+b^2 )}\)
sin\(⁡(β) =\ \frac{b}{c}= \frac{b}{\sqrt{(a^2+b^2 )}}\)

4- C
\(|\frac{x}{2}-2x+10|<5 \)
\(|- \frac{3}{2}x -2x+10|<5\)
\(-5<-\frac{3}{2}x +10<5\)
Subtract 10 from all sides of the inequality. \(→-5-10<- \frac{3}{2}x +10-10<5-10→-15<- \frac{3}{2}x x<-5 \)
Multiply all sides by 2. \(→2×(-15)<2×(-\frac{3x}{2})<2×(-5)→-30<-3x<-10\) Divide all sides by \(-3\). (Remember that when you divide all sides of an inequality by a negative number, the inequality sign will be swapped. < becomes >)
\(→\frac{-30}{-3}>\frac{-3x}{-3}>\frac{-10}{-3}\)
\(\frac{10}{3}\ < x <10\)

5- 1
The intersection of two functions is the point with 2 for \(x\). Then:
\(f(2)=g(2) \space and \space g(2)=(2×(2))-3=4-3=1\)
\(Then, f(2)=1→a(2)^2+b(2)+c=1→4a+2b+c=1 (i)\)
The value of x in the vertex of the parabola is:
\(x=- \frac{b}{2a}→-2=- \frac{b}{2a}→b=4a \space (ii)\)
In the point (-2, 5), the value of the \(f(x)\) is 5.
\(f(-2)=5→a(-2)^2+b(-2)+c=5→4a-2b+c=5 (iii)\)
Using the first two equations:
\(4a+2b+c=1\)
\(4a-2b+c=5\)
Equation 1 minus equation 2 is:
\((i)-(iii) →4b=-4→b=-1 \space \space (iv)\)
Plug in the value of b in the second equation:
\(b=4a →a =\frac{b}{4}= – \frac{1}{4}\)
Plug in the values of a and be in the first equation. Then:
\(4 (-\frac{1}{4}) +2(-1)+c=1→-1-2+c=1→c=1+3→c=4\)
the product of a, b and c= \(-\frac{1}{4}) ×(-1)×4=1\)

6- 60
The relationship among all sides of the special right triangle
\(30^\circ-60^\circ- 90^\circ\) is provided in this triangle:

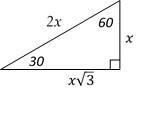
In this triangle, the opposite side of \(30^\circ\) angle is half of the hypotenuse.

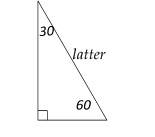
Draw the shape of this question:
The latter is the hypotenuse. Therefore, the latter is 60 ft.

7- 3
Let \(x\) be the length of an edge of a cube, then the volume of a cube is: \(V=x^3 \)
The surface area of a cube is:
\(SA=6x^2\)
The volume of cube A is \(1/2\) of its surface area. Then:
\(x^3 = \frac{6x^2}{2}→x^3=3x^2\)
divide both sides of the equation by \(x^2\). Then:
\(\frac{x^3}{x^2} = \frac{3x^2}{x^2} →x=3\)

8- 5
Multiply both sides by \(x\).
\(x×(3x+6y)=x× (\frac{-3y^2+15}{x})→3x^2+6xy=-3y^2+15 \)
\(→3x^2+6xy+3y^2=15→3×(x^2+2xy+y^2 )=15→x^2+2xy+y^2= \frac{15}{3}\)
\(x^2+2xy+y^2=(x+y)^2, Then:\)
\(→(x+y)^2=5\)

9- D
\(3x – 5= 8.5 → 3x = 8.5 + 5 = 13.5 → x = \frac{13.5}{3}= 4.5\)
Then; \(5x + 3 = 5 (4.5) + 3 = 22.5 + 3 = 25.5\)

10- B
Number of biology books: \(35\)
Total number of books; \(35+95+80=210\)
the ratio of the number of biology books to the total number of books is:
\(\frac{35}{210}= \frac{1}{6}\)

11- B
\(α=180^\circ-112^\circ=68^\circ\)
\( β=180^\circ-135^\circ=45^\circ\)
\( x+α+β=180^\circ→x=180^\circ-68^\circ-45^\circ=67^\circ\)

12- D
A. \(f(x)=x^2-5 \space if \ x=1→f(1)=(1)^2-5=1-5=-4≠5 \)
B. \(f(x)=x^2-1 \space if \ x=1→f(1)=(1)^2-1=1-1=0≠5 \)
C. \(f(x)=\sqrt{(x+2)} \space if \ x=1→f(1)=\sqrt{(1+2)}=\sqrt 3≠5\)
D. \(f(x)=\sqrt{x}+4 \space if \ x=1→f(1)=\sqrt 1+4=5\)

13- D
\(xp+2yq=26→xp=26-2yq \space (1)\)
\(xp+yq=17 \space (2)\)
\((1) \space in \space (2) →26-2yq+yq=17→26-yq=17→yq=26-17=9\)

14- D
Let \(x\) be all expenses, then
\(\frac{22}{100}x =$660 →x= \frac{100×$660}{22}=$3000\)
He spent for his rent: \(\frac{27}{100}×$3000 = $810\)

15- A
\(12x^2+n=a(x^2+3)(x^2-3)=ax^4-9a→a=12 \)
And
\(n=-9a=-9×12=-108\)

16- C
\(\frac{1}{8}= 0.125→C=5\)
\(\frac{1}{20}=0.05→D=5→C×D=5×5=25\)

17- C
Let P be the circumference of circle A, then;
\(2πr_{A}=18π→r_{A}=9\)
\(r_{A} = 3 r_{B}→r_{B}= \frac{9}{3} = 3\)
→ Area of circle B is;
\(πr^2_{B}=9π\)

18- B
\(f(x)=x^2+2x-5\)
\(f(3t^2 )=(3t^2 )^2+2(3t^2 )-5=9t^4+6t^2-5\)

19- C
\(y\) is the intersection of the three circles. Therefore, it must be odd (from circle A), negative (from circle B), and multiple of 5 (from circle C).
From the options, only\( -5\) is odd, negative, and multiple of 5.

20- C
let \(x\) be the total number of marbles in the box, then the number of red marbles is: \(x – 132\)
\(p = \frac{1}{4}= \frac{x – 132}{x}\)
Use cross multiplication to solve for \(x\).
\( x=4(x-132)→x=4x-528→3x=528→x=176 \)

College Entrance Tests

Looking for the best resource to help you succeed on the PSAT Math test?

The Best Books to Ace the PSAT Math Test