How to Find the Surface Area of Pyramid?

A pyramid is a three-dimensional shape whose base is polygonal and whose sides (which are triangles) meet at a point called the apex (or) vertex. The perpendicular distance from the vertex to the center of the base is called the altitude or height of the pyramid. The length of the perpendicular drawn from the apex to the base of a triangle (side face) is called the slant height.

Related Topics

• How to Find the Volume of Cones and Pyramids?

A step-by-step guide to finding the surface area of a pyramid

The surface area of a pyramid is the measure of the total area occupied by all its facets.

The surface area of a pyramid is the sum of the area of its faces and hence it is measured in square units. A pyramid has two types of surface areas, one is the Lateral Surface Area \((LSA)\) and the other is the Total Surface Area \((TSA)\).

• The Lateral Surface Area \((LSA)\) of a pyramid \(=\) The sum of areas of the side faces (triangles) of the pyramid.
• The Total Surface Area \((TSA)\) of a pyramid \(= LSA\) of pyramid \(+\) Base area

Note: The surface area of a pyramid without any specifications refers to the total surface area of the pyramid.

The surface area of a pyramid formula

We can calculate the surface area of a pyramid by finding the area of each of its faces and their sum. If the pyramid is regular, there are special formulas for finding the lateral surface area and total surface area.

Consider a regular pyramid with a base perimeter of \(P\), a base area of \(B\), and a slant height of (height of each triangle) \(l\). Then,

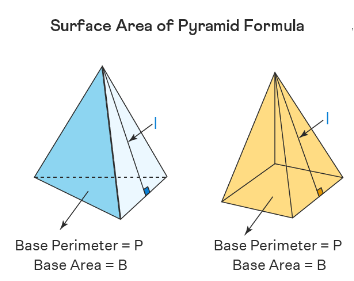
• \(\color {blue}{LSA= \frac{1}{2} Pl}\)
• \(\color{blue}{TSA = LSA + base\:area = \frac{1}{2} Pl + B}\)

Note that here we use the polygon area formula to calculate the base area.

Finding the Surface Area of Pyramid – Example 1:

The side length of the base is \(15\) inches and the slant height of the pyramid is \(18\) inches. Calculate the lateral surface area of a square pyramid.

Solution:

The side length of the base, \(a=15\) inches

Then, the perimeter of the base (square) is \(P = 4a = 4(15) = 60\) inches.

Slant height, \(l= 18\) inches

The lateral surface area of a square pyramid is,

\(LSA = \frac{1}{2}Pl\)

\(= \frac{1}{2} × (60) × 18\)

\(= 540\space in^2\)

Exercises for Finding the Surface Area of Pyramid

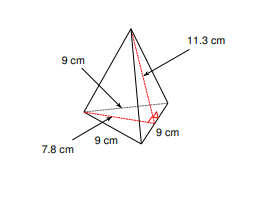
• Find the lateral area and surface area of each figure. Round your answers to the nearest tenth

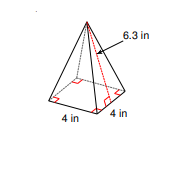
• \(\color{blue}{50.4\space in^2, 66.4 \space in^2 }\)
• \(\color{blue}{152.6\space cm^2, 187.7 \space cm^2 }\)