10 Most Common SIFT Math Questions

Preparing for the SIFT Math test? Want a preview of the most common mathematics questions on the SIFT Math test? If so, then you are in the right place.
The mathematics section of SIFT can be a challenging area for many test-takers, but with enough patience, it can be easy and even enjoyable!
Preparing for the SIFT Math test can be a nerve-wracking experience. Learning more about what you’re going to see when you take the SIFT can help to reduce those pre-test jitters. Here’s your chance to review the 10 most common SIFT Math questions to help you know what to expect and what to practice most. Try these 10 most common SIFT Math questions to hone your mathematical skills and to see if your math skills are up to date on what’s being asked on the exam or if you still need more practice.
Make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions you need to practice.
The Absolute Best Book to Ace the SIFT Math Test
10 Sample SIFT Math Practice Questions
1- Simplify \(6x^2 y^3 (2x^2 y)^3= \)
A. \(12x^4 y^6\)
B. \(12x^8 y^6\)
C. \(48x^4 y^6\)
D. \(48x^8 y^6\)
2- The diagonal of a rectangle is 10 inches long and the height of the rectangle is 8 inches. What is the perimeter of the rectangle in inches?______
3-What is the value of x in the following equation?
\( \frac{2}{3} x+\frac{1}{6}= \frac{1}{3} \)
A. \(6\)
B. \(\frac{1}{2} \)
C. \(\frac{1}{3} \)
D. \(\frac{1}{4} \)
4- A card is drawn at random from a standard 52–card deck, what is the probability that the card is of Hearts? (The deck includes 13 of each suit clubs, diamonds, hearts, and spades)
A. \(\frac{1}{3} \)
B. \(\frac{1}{6} \)
C. \(\frac{1}{52} \)
D. \(\frac{1}{4} \)
5- Which of the following shows the numbers in ascending order?
\(\frac{2}{3} , 0.68 , 67\% , \frac{4}{5}\)
A. \(67\%, 0.68, \frac{2}{3} , \frac{4}{5} \)
B. \(67\%, 0.68, \frac{4}{5}, \frac{2}{3} \)
C. \(0.68, 67\%, \frac{2}{3}, \frac{4}{5} \)
D. \(\frac{2}{3}, 67\%, 0.68, \frac{4}{5} \)
6- The mean of 50 test scores was calculated as 88. But, it turned out that one of the scores was misread as 94 but it was 69. What is the mean?
A. 85
B. 87
C. 87.5
D. 88.5
7- Two dice are thrown simultaneously, what is the probability of getting a sum of 6 or 9?
A. \(\frac{1}{3} \)
B. \(\frac{1}{4} \)
C. \(\frac{1}{6} \)
D. \(\frac{1}{2} \)
8- Jason is 9 miles ahead of Joe running at 5.5 miles per hour and Joe is running at the speed of 7 miles per hour. How long does it take Joe to catch Jason?
A. 3 hours
B. 4 hours
C. 6 hours
D. 8 hours
9- 55 students took an exam and 11 of them failed. What percent of the students passed the exam?
A. \(40\%\)
B. \(60\%\)
C. \(80\%\)
D. \(20\%\)
10- What is the volume of a box with the following dimensions?
Height = 4 cm Width = 5 cm Length = 6 cm
A. 15 cm\(^3\)
B. 60 cm\(^3\)
C. 90 cm\(^3\)
D. 120 cm\(^3\)
Best SIFT Math Prep Resource for 2022
Answers:
1- D
Simplify.
\(6x^2 y^3 (2x^2 y)^3= 6x^2 y^3 (8x^6 y^3 ) = 48x^8 y^6\)
2- 28
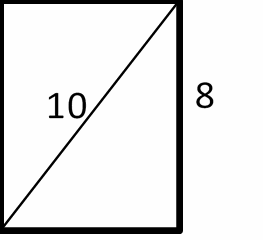
Let \(x\) be the width of the rectangle. Use Pythagorean Theorem:
\(a^2 + b^2 = c^2\)
\(x^2 + 8^2 = 10^2 {\Rightarrow} x^2 + 64 = 100 {\Rightarrow} x^2 = 100 – 64 = 36 ⇒ x = 6\)
Perimeter of the rectangle = 2 (length + width) = 2 (8 + 6) = 2 (14) = 28
3- D
Isolate and solve for \(x\).
\(\frac{2}{3} x+\frac{1}{6} = \frac{1}{3} {\Rightarrow} \frac{2}{3} x= \frac{1}{3} -\frac{1}{6} = \frac{1}{6} {\Rightarrow} \frac{2}{3} x= \frac{1}{6} \)
Multiply both sides by the reciprocal of the coefficient of \(x\).
\((\frac{3}{2}) \frac{2}{3} x= \frac{1}{6} (\frac{3}{2}) {\Rightarrow} x= \frac{3}{12}=\frac{1}{4}\)
4- D
The probability of choosing a Hearts is \(\frac{13}{52}=\frac{1}{4} \)
5- D
Change the numbers to decimal and then compare.
\(\frac{2}{3} = 0.666… \)
\(0.68 \)
\(67\% = 0.67\)
\(\frac{4}{5} = 0.80\)
Therefore
\(\frac{2}{3} < 67\% < 0.68 < \frac{4}{5}\)
6- C
average (mean) =\(\frac{(sum \space of \space terms)}{(number \space of \space terms)} {\Rightarrow} 88 = \frac{(sum \space of \space terms)}{50} {\Rightarrow} sum\) =\( 88 {\times} 50 = 4400\)
The difference of 94 and 69 is 25. Therefore, 25 should be subtracted from the sum.
\(4400 – 25 = 4375\)
mean =\( \frac{(sum of terms)}{(number of terms)} ⇒\) mean =\(\frac{(4375)}{50}= 87.5\)
7- B
To get a sum of 6 for two dice, we can get 5 different options:
(5, 1), (4, 2), (3, 3), (2, 4), (1, 5)
To get a sum of 9 for two dice, we can get 4 different options:
(6, 3), (5, 4), (4, 5), (3, 6)
Therefore, there are 9 options to get the sum of 6 or 9.
Since, we have 6 × 6 = 36 total options, the probability of getting a sum of 6 and 9 is 9 out of 36 or \(\frac{1}{4}\).
8- C
The distance between Jason and Joe is 9 miles. Jason running at 5.5 miles per hour and Joe is running at the speed of 7 miles per hour. Therefore, every hour the distance is 1.5 miles less. 9 \(\div \) 1.5 = 6
9- C
The failing rate is 11 out of 55 = \(\frac{11}{55} \)
Change the fraction to percent:
\(\frac{11}{55} {\times} 100\%=20\%\)
20 percent of students failed. Therefore, 80 percent of students passed the exam.
10- D
Volume of a box = length \(\times \) width \(\times \) height = 4 \(\times \) 5\(\times \) 6 = 120
The Best Books to Ace the SIFT Math Test
Related to This Article
More math articles
- 6th Grade MAAP Math Worksheets: FREE & Printable
- SSAT Middle-Level Math Worksheets: FREE & Printable
- 4th Grade LEAP Math Worksheets: FREE & Printable
- How to Solve an Absolute Value Inequality?
- Top 10 6th Grade ACT Aspire Math Practice Questions
- A Comprehensive Collection of Free AFOQT Math Practice Tests
- Full-Length 8th Grade ACT Aspire Math Practice Test-Answers and Explanations
- 7th Grade IAR Math Worksheets: FREE & Printable
- FTCE General Knowledge Test Review
- Top 10 Pre-Algebra Prep Books (Our 2024 Favorite Picks)



















What people say about "10 Most Common SIFT Math Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.