Trigonometric Ratios

Related Topics

• How to Evaluate Trigonometric Function?

A step-by-step guide to trigonometric ratios

Trigonometric ratios are the ratio of the lengths of the sides of a triangle. These ratios in trigonometry relate the ratio of the sides of a right triangle to the corresponding angle. There are six trigonometric ratios, namely, sine, cosine, tangent, secant, cosecant, and cotangent. These ratios are written as \(sin\), \(cos\), \(tan\), \(sec\), \(cosec\) (or \(csc\)), and \(cot\) in short.

The values of these trigonometric ratios can be calculated using the measurement of an acute angle, \(θ\), in a right triangle.

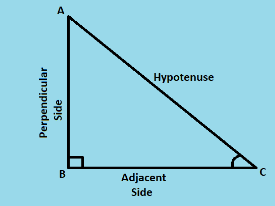
What are trigonometric ratios?

These six trigonometric ratios can be defined as:

Sine: In the given triangle, the \(sin\) of the angle \(θ\) can be considered as follows, \(\color{blue}{sin\: θ = \frac{AB}{AC}}\).

Cosine: In the given triangle, the \(cos\) of the angle \(θ\) can be considered as follows, \(\color{blue}{cos\: θ = \frac{BC}{AC}}\).

Tangent: In the given triangle, the \(tan\) of the angle \(θ\) can be considered as follows, \(\color{blue}{tan\: θ = \frac{AB}{BC}}\).

Cosecant: In the given triangle, the \(cosec\) of the angle \(θ\) can be considered as follows, \(\color{blue}{cosec\: θ = \frac{AC}{AB}}\).

Secant: In the given triangle, the \(sec\) of the angle \(θ\) can be considered as follows, \(\color{blue}{sec\: θ = \frac{AC}{BC}}\).

Cotangent: In the given triangle, the \(cot\) of the angle \(θ\) can be considered as follows, \(\color{blue}{cot\: θ = \frac{BC}{AB}}\).

Trigonometric ratios formulas

We can use the shorthand form of trigonometric ratios to compare the length of both sides with the base angle. The angle \(θ\) is acute \((θ<90º)\) and in general is measured with reference to the positive \(x\)-axis, in the anticlockwise direction. The basic trigonometric ratio formulas are given below,

• \(\color{blue}{sin\: θ = \frac{Perpendicular}{Hypotenuse}}\)
• \(\color{blue}{cos\: θ = \frac{Base}{Hypotenuse}}\)
• \(\color{blue}{tan\: θ = \frac{Perpendicular}{Base}}\)
• \(\color{blue}{sec\: θ =\frac{Hypotenuse}{Base}}\)
• \(\color{blue}{cosec\: θ = \frac{Hypotenuse}{Perpendicular}}\)
• \(\color{blue}{cot\: θ = \frac{Base}{Perpendicular}}\)

Trigonometric Ratios – Example 1:

Find the value of \(tan\:θ\) if \(sin\:θ\:=\frac{10}{3}\) and \(cos\:θ\:=\frac{5}{3}\:\).

Solution: Use the formula of the trigonometric ratio to solve this problem: \(tan\: θ = \frac{Perpendicular}{Base}\).

\(tan\:θ =\frac {10}{5}=2\)