Everything You Need to Know About Sketching Curves Using Derivatives

Overview:

The first derivative test involves examining where the derivative changes sign to identify local maxima and minima: a function is increasing where its derivative is positive and decreasing where it’s negative.

The second derivative test further refines this analysis. A positive second derivative implies the graph is concave up, suggesting a local minimum; a negative second derivative indicates concave down, pointing to a local maximum.

Additionally, points where the second derivative changes sign are inflection points, marking transitions between concave up and down. Together, these tests provide a comprehensive toolkit for analyzing a function’s behavior and identifying key features of its graph.

Except for situations where the first derivative is zero or undefined and the second derivative test is inconclusive. In such cases, further analysis or alternative methods, like the first derivative test or examining function values around the critical point, might be needed to accurately determine the nature of the extrema. Additionally, if the second derivative is zero or undefined at a point, it may not conclusively indicate an inflection point, requiring additional investigation.

(An inflection point is where a function’s graph changes concavity, shifting from concave up to concave down, or vice versa.)

Example:

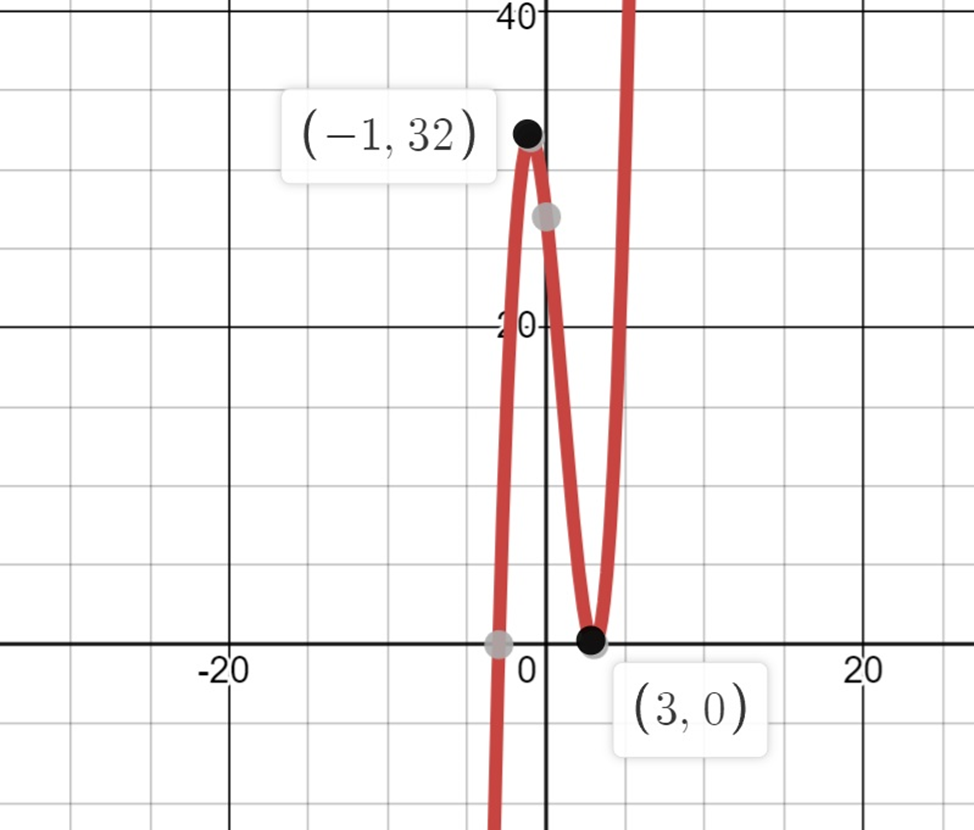
\( \text{Analyze and sketch the curve of } f(x) = x^3 – 3x^2 – 9x + 27. \)

First Derivative (for critical points and slope):

\( f(x) = x^3 – 3x^2 – 9x + 27 \)

\( f'(x) = 3x^2 – 6x – 9 \)

Find Critical Points(\(x\) points where first derivative is zero):

\( 3x^2 – 6x – 9 = 0 \)

After solving this using delta method (\( [(b^2)-4ac] \), we get \( 3 \) and \( -1 \) as the results. At these points, first derivative is zero.

So it’s decreasing at \( x=-1 \) until it reaches \( 3 \), [meaning it was increasing before \( -1 \)

and it’s increasing from \( x=3 \).

Second Derivative (for concavity and points of inflection):

\( f”(x) = 6x – 6 \)

\( 6x – 6 = 0 \)

So at \( x=1 \), concavity changes.

Let’s take a look at the functions graph:

Complete Curve Sketching Using Derivative Analysis

Curve sketching synthesizes calculus tools, the first derivative revealing increasing/decreasing intervals and local extrema, the second derivative showing concavity and inflection points, with geometric visualization. Mastering this skill means you can sketch accurate curves without extensive point-by-point plotting, relying instead on systematic derivative analysis.

The Five-Step Curve Sketching Methodology

Step One involves finding all critical points where f'(x) = 0 or where the derivative is undefined. These points represent candidates for local maxima and minima. Step Two determines whether the function increases or decreases on intervals created by critical points. Test the sign of f'(x) at sample points in each interval; positive values indicate increasing regions, negative values indicate decreasing regions. Step Three involves finding the second derivative f”(x) and locating points where it equals zero or is undefined. These are candidate inflection points. Step Four determines concavity by testing the sign of f”(x). Positive second derivative indicates concave-up curves (shaped like valleys), negative indicates concave-down curves (shaped like hills). Step Five calculates function values at critical points and inflection points to obtain coordinates for accurate curve sketching.

Worked Example: Cubic Function Analysis

Consider f(x) = x³ – 3x² + 2. The first derivative is f'(x) = 3x² – 6x = 3x(x – 2). Setting this equal to zero yields critical points at x = 0 and x = 2. Test the sign of f'(x) at sample points: for x = -1, f'(-1) = 3(-1)(-3) = 9, which is positive, indicating the function increases on (-∞, 0). For x = 1, f'(1) = 3(1)(-1) = -3, which is negative, indicating decrease on (0, 2). For x = 3, f'(3) = 3(3)(1) = 9, which is positive, indicating increase on (2, ∞). Therefore x = 0 is a local maximum and x = 2 is a local minimum.

The second derivative is f”(x) = 6x – 6. Setting this equal to zero yields x = 1. Testing: f”(0) = -6, which is negative (concave down). F”(2) = 6, which is positive (concave up). The function changes from concave-down to concave-up at x = 1, making this an inflection point. Calculate coordinates: f(0) = 2 (local max), f(2) = -2 (local min), f(1) = 0 (inflection point).

Key Information Extracted from Derivatives

From f'(x): identify critical points, determine increasing/decreasing intervals, classify local extrema as maxima or minima. From f”(x): identify inflection point candidates, determine concavity intervals, confirm actual inflection points where concavity changes. The combination of this information produces a complete picture of curve behavior without requiring the calculation of many individual points.

Common Mistakes and Prevention

Confusing critical points with extrema: not all critical points are maxima or minima, use the first derivative test to classify. Missing points where f'(x) is undefined: critical points include both where f'(x) = 0 and where the derivative doesn’t exist. Assuming inflection points at every f”(x) = 0: you must verify that concavity actually changes. Not evaluating the function at key points: you need coordinates for accurate sketching, not just x-values of critical points.

For comprehensive calculus study, visit our ultimate calculus course which includes additional curve sketching examples and applications.

Complete Curve Sketching Using Derivative Analysis

Curve sketching synthesizes calculus tools, the first derivative revealing increasing/decreasing intervals and local extrema, the second derivative showing concavity and inflection points, with geometric visualization. Mastering this skill means you can sketch accurate curves without extensive point-by-point plotting, relying instead on systematic derivative analysis.

The Five-Step Curve Sketching Methodology

Step One involves finding all critical points where f'(x) = 0 or where the derivative is undefined. These points represent candidates for local maxima and minima. Step Two determines whether the function increases or decreases on intervals created by critical points. Test the sign of f'(x) at sample points in each interval; positive values indicate increasing regions, negative values indicate decreasing regions. Step Three involves finding the second derivative f”(x) and locating points where it equals zero or is undefined. These are candidate inflection points. Step Four determines concavity by testing the sign of f”(x). Positive second derivative indicates concave-up curves (shaped like valleys), negative indicates concave-down curves (shaped like hills). Step Five calculates function values at critical points and inflection points to obtain coordinates for accurate curve sketching.

Worked Example: Cubic Function Analysis

Consider f(x) = x³ – 3x² + 2. The first derivative is f'(x) = 3x² – 6x = 3x(x – 2). Setting this equal to zero yields critical points at x = 0 and x = 2. Test the sign of f'(x) at sample points: for x = -1, f'(-1) = 3(-1)(-3) = 9, which is positive, indicating the function increases on (-∞, 0). For x = 1, f'(1) = 3(1)(-1) = -3, which is negative, indicating decrease on (0, 2). For x = 3, f'(3) = 3(3)(1) = 9, which is positive, indicating increase on (2, ∞). Therefore x = 0 is a local maximum and x = 2 is a local minimum.

The second derivative is f”(x) = 6x – 6. Setting this equal to zero yields x = 1. Testing: f”(0) = -6, which is negative (concave down). F”(2) = 6, which is positive (concave up). The function changes from concave-down to concave-up at x = 1, making this an inflection point. Calculate coordinates: f(0) = 2 (local max), f(2) = -2 (local min), f(1) = 0 (inflection point).

Key Information Extracted from Derivatives

From f'(x): identify critical points, determine increasing/decreasing intervals, classify local extrema as maxima or minima. From f”(x): identify inflection point candidates, determine concavity intervals, confirm actual inflection points where concavity changes. The combination of this information produces a complete picture of curve behavior without requiring the calculation of many individual points.

Common Mistakes and Prevention

Confusing critical points with extrema: not all critical points are maxima or minima, use the first derivative test to classify. Missing points where f'(x) is undefined: critical points include both where f'(x) = 0 and where the derivative doesn’t exist. Assuming inflection points at every f”(x) = 0: you must verify that concavity actually changes. Not evaluating the function at key points: you need coordinates for accurate sketching, not just x-values of critical points.

For comprehensive calculus study, visit our ultimate calculus course which includes additional curve sketching examples and applications.

Recommended EffortlessMath Books

For a workbook that builds graphing intuition before calculus, the Pre-Calculus for Beginners covers functions, transformations, asymptotes, and graphing with worked examples. For the algebra foundation, the Algebra II for Beginners drills the polynomial and rational-function skills curve sketching depends on.

Pre-Calculus for Beginners 2026 The Ultimate Step by Step Guide to Acing Precalculus

Download

$27.99 Original price was: $27.99.$17.99Current price is: $17.99.

Frequently Asked Questions

What is curve sketching in calculus?

Curve sketching in calculus means drawing an accurate graph of a function by analyzing it rather than plotting many random points. You find the domain, intercepts and asymptotes, then use the first derivative to locate where the function rises, falls and has local maximums or minimums, and the second derivative to find concavity and inflection points.

How do you sketch a graph using derivatives?

Work through a checklist. First note the domain, intercepts and any vertical or horizontal asymptotes. Next solve f′(x) = 0, and find where f′ is undefined, to get critical points, then test the sign of f′ between them. Then solve f″(x) = 0 and test the sign of f″ to find concavity. Finally plot these key points and connect them with the right shape.

What are the rules of curve sketching?

The key rules: if f′(x) > 0 the graph rises, and if f′(x) < 0 it falls. A sign change in f′ from positive to negative marks a local maximum, and from negative to positive a local minimum. If f″(x) > 0 the curve is concave up, and if f″(x) < 0 it is concave down. An inflection point needs f″ to actually change sign, not just equal zero.

What is an example of curve sketching?

Sketch f(x) = x³ − 3x. Here f′(x) = 3x² − 3, which is zero at x = −1 and x = 1. Since f(−1) = 2 and f(1) = −2, there is a local maximum at (−1, 2) and a local minimum at (1, −2). Then f″(x) = 6x, so the inflection point is (0, 0). The x-intercepts are 0 and ±√3.

How do you sketch a derivative from a graph?

Read the slope of the original graph. Wherever f has a horizontal tangent, f′ crosses or touches zero. Where f is rising, draw f′ above the x-axis, and where f is falling, draw it below. The steepest parts of f become the highest or lowest points of f′, and inflection points of f become local maximums or minimums of f′.

Related EffortlessMath Lessons

If a topic on this page feels rusty, these short lessons go deeper:

• Second derivatives
• Product rule
• Derivative of log functions
• Vector function derivatives
• Derivatives of polar coordinates