How to Write Linear Equations from Graphs

A linear equation represents a straight line on a two-dimensional plane, typically illustrated on a graph with the \(x\) and \(y\)-axes. A standard form of a linear equation is \(y = mx + b\), where ‘\(m\)’ stands for the slope and ‘\(b\)’ is the \(y\)-intercept.

A graph is a visual representation of a mathematical function or a set of data. The horizontal axis, often labeled ‘\(x\),’ and the vertical axis, labeled ‘\(y\),’ intersect at a point called the origin.

A Step-by-step Guide to Writing Linear Equations from Graphs

Here’s a step-by-step guide on Write Linear Equations from Graphs:

Step 1: Identify the Slope and the Y-Intercept

In a linear equation, the slope (‘\(m\)’) is the measure of the tilt of the line – a ratio of vertical change (the rise) to horizontal change (the run). On the other hand, the \(y\)-intercept (‘\(b\)’) is the point where the line intersects the \(y\)-axis. It represents the value of ‘\(y\)’ when ‘\(x\)’ equals zero.

Step 2: Determine the Slope

The slope can be determined from the graph by selecting any two points on the line. The formula for finding the slope is \(m =\frac{(y_2 – y_1)}{(x_2 – x_1)}\). This formula represents the ratio of the difference in ‘\(y\)’ coordinates (vertical change) to the difference in ‘\(x\)’ coordinates (horizontal change).

Step 3: Determine the Y-Intercept

The \(y\)-intercept can be identified visually on the graph as the point where the line crosses the \(y\)-axis. The coordinate of this point always has ‘\(x\)’ equal to zero.

Step 4: Write the Linear Equation

Now, with the slope (‘\(m\)’) and \(y\)-intercept (‘\(b\)’) identified, you can write the linear equation. Substitute these values into the equation \(y = mx + b\).

Practical Example: Writing a Linear Equation from a Graph

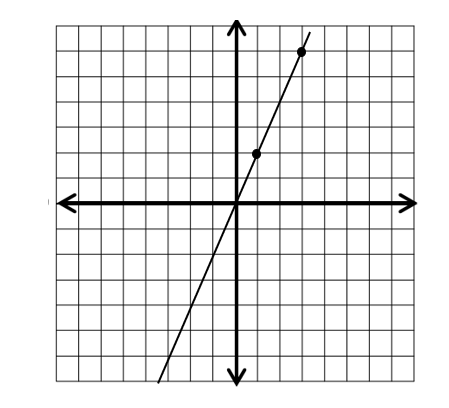
Consider a graph with two points \(A(1,2)\) and \(B(3,6)\). The slope of the line \(AB\) is \(m = \frac{(6-2)}{(3-1) }= 2\). The line intersects the \(y\)-axis at \((0,0)\), which means the \(y\)-intercept \(b = 0\). Therefore, the linear equation for this line would be \(y = 2x + 0\) or simply \(y = 2x\).

Conclusion

Understanding how to write linear equations from graphs is a skill with many practical applications. It aids in understanding the behavior of mathematical functions and provides a solid foundation for exploring more complex areas of mathematics. Whether you’re a student, a professional, or just curious about math, mastering this skill can open the door to a greater understanding of the world around us.

Remember, the key to mastering any complex concept is practice. We hope this guide has provided you with the confidence and understanding to interpret graphs and write linear equations accurately.