Full-Length TABE 11 & 12 Math Practice Test-Answers and Explanations

Did you take the TABE 11 & 12 Math Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.

TABE 11 & 12 Math Practice Test Answers and Explanations

Part 1: Mathematics Computation

1- Choice C is correct
\(14 × 6 = 84\)

2- Choice C is correct
\(748 + 37 = 785\)

3- Choice B is correct
\(1,147 + 687 = 1,834\)

4- Choice B is correct
\(378 – 132 = 246\)

5- Choice C is correct
\(1,983 – 362 = 1,621\)

6- Choice C is correct
\(198 + 2,295 = 2,493\)

7- Choice B is correct
\(7,000 ÷ 200 = 35\)

8- Choice A is correct
\(2,357 – 1,649 = 708\)

9- Choice B is correct
\(78.32 +15.73 = 94.05\)

10- Choice B is correct
\(3.6+6.1=9.7\)

11- Choice A is correct
\(32.17 – 27.65 = 4.52\)

12- Choice C is correct
\(\cfrac{\begin{align} 5.8 \\ × 3.4 \end{align}}{23.12} \)

13- Choice C is correct
\(17.8÷100=0.178\)

14- Choice B is correct
\(450÷6=75\)

15- Choice B is correct
\(9ab – 2ab=7ab\)

16- Choice C is correct
\(\frac{3}{5}+\frac{4}{5}=\frac{7}{5}\)

17- Choice D is correct
\(14 –(–6)=14+6=20\)

18- Choice B is correct
\(13.5÷4.5=3\)

19- Choice D is correct
\(148 ÷ 4 = 37\)

20- Choice B is correct
\(2,768 ÷ 8 = 346\)

The Absolute Best Book to Ace the TABE 11 & 12 Math Test

21- Choice B is correct
\(-3+9-4= 2\)

22- Choice B is correct
\(\frac{5}{7}-\frac{2}{7}=\frac{3}{7}\)

23- Choice D is correct
\(\frac{3}{5}+\frac{2}{5}=\frac{5}{5}=1\)

24- Choice A is correct
\(\frac{3}{7}×\frac{2}{5}=\frac{6}{35}\)

25- Choice B is correct
\(7^3× 7^4=7^7\)

26- Choice D is correct
\(3 \frac{1}{5}×5 \frac{2}{3}= \frac{16}{5}×\frac{17}{3}=\frac{272}{15}=18 \frac{2}{15}\)

27- Choice C is correct
\(3 \frac{2}{5}+5 \frac{1}{2}=8 \frac{9}{10}\)

28- Choice B is correct
\(5 \frac{3}{4}-3 \frac{1}{4}=5+\frac{3}{4}-3-\frac{1}{4}=2 \frac{2}{4}=2 \frac{1}{2}\)

29- Choice B is correct
\(4 \frac{3}{5}-\frac{1}{2}=4 \frac{1}{10}\)

30- Choice C is correct
\(\frac{3}{7}÷\frac{2}{5}=\frac{15}{14}\)

31- Choice B is correct
\(3^3× 3^4=3^{3+4}= 3^7\)

32- Choice A is correct
\(3 \frac{2}{7}÷2 \frac{2}{5}=\frac{23}{7} ÷\frac{12}{5}= \frac{115}{84}=1 \frac{31}{84}\)

33- Choice C is correct
\(15\%\) of \(60\) \(= 0.15 × 60 = 9\)

34- Choice B is correct
\(20\%\) of \(20\) \(= 0.2 × 20 = 4\)

35- Choice C is correct
\(25 \%\) of \(40 = 10\)

36- Choice A is correct
\(6\%\) of __ \(= 36, \frac{6}{100} × x = 36, \frac{6x}{100}=36, x=\frac{3,600}{6}=600\)

37- Choice D is correct
\(7x+4x=11x\)

38- Choice B is correct
\(8×(-3)=-24\)

39- Choice C is correct
\(9ab-ab=8ab\)

40- Choice A is correct
\(73.50÷3.75=19.6\)

Part 2: Applied Mathematics

41- Choice B is correct
\(3^5=3×3×3×3×3=243\)

42- Choice B is correct
A. \(\frac{1}{5}=0.2\)
B. \(\frac{2}{3}=0.67\)
C. \(\frac{4}{7}=0.57\)
D. \(\frac{1}{2}=0.5\)

43- Choice B is correct
\(\frac{11+ 23+17+27+7}{5}=\frac{85}{5}=17\)

44- Choice A is correct
Use PEMDAS (order of operation):
\(-9-3×(–3)+[-3+11×(-3)]÷2=-9+9+[-3-33]÷2=0+[-36]÷2=-36÷2=-18\)

45- Choice C is correct
\(160÷20=8\)

46- Choice B is correct
\(x + y = N → x = 5 → 5 + y = N → y = N –5 → 5y = 5(N – 5)\)

47- Choice D is correct
\($15×10=$150\) → Petrol use: \(10×3=30\) liters → Petrol cost: \(30×$2=$60\)
Money earned: \($150-$60=$90\)

48- Choice A is correct
\(2x+3=7.2→2x=7.2-3=4.2→x=\frac{4.2}{2}=2.1\)
Then; \(3x-5=3(2.1)-5=6.3-5=1.3\)

49- Choice C is correct
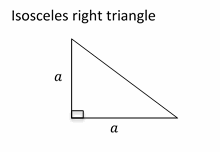
First, draw an isosceles triangle. Remember that the two sides of the triangle are equal.
Let put a for the legs. Then:
\(a=8\) ⇒ area of the triangle is \(=\frac{1}{2}(8×8)=\frac{64}{2}=32 \space cm^2\)

50- Choice C is correct
Write the numbers in order: 3, 5, 11, 15, 19, 21, 25
Since we have 7 numbers (7 is odd), then the median is the number in the middle, which is 15.

51- Choice D is correct
To find the discount, multiply the number by \((100\% – \)rate of discount)\).
Therefore, for the first discount we get: \((420)(100\% –17\%)=(420)(0.83)\)
For the next 13% discount: \((420)(0.83)(0.87)\)

52- Choice C is correct
Plug in each pair of numbers in the equation: \(2x-3y=5\)
A. \((-2,1): ⇒2 (-2) -3 (1) = -7\)
B. \((–1,3): ⇒2 (–1) -3 (3) = -11\)
C. \(( 4,1): ⇒2 (4) -3 (1) = 5\)
D. \((2,2): ⇒2 (3) -3 (2) = 0\)
Choice C is correct.

53- Choice D is correct
average \(=\frac{sum \space of \space terms}{number \space of \space terms} ⇒ 25=\frac{21+18+17+x}{4} ⇒100=56+x ⇒ x=44\)

54- Choice A is correct
Use this formula: Percent of Change: \(\frac{New \space Value-Old \space Value}{Old \space Value}×100\%\)
\(\frac{25500-30000}{30000}×100\%=15\% \space and \space \frac{21678-25500}{25500}×100\%=15\%\)

55- Choice C is correct
Let \(x\) be the original price. If the price of the sofa is decreased by \(16\%\) to $378, then: \(84\%\) of \(x=378 ⇒ 0.84x=378 ⇒ x=378÷0.84=450\)

56- Choice C is correct
The sum of supplement angles is 180. Let \(x\) be that angle. Therefore, \(x+7x=180\)
\(8x=180\), divide both sides by 8: \(x=22.5\)

57- Choice D is correct
The average speed of john is: \(120÷4=30\) km
The average speed of Alice is: \(180÷5=36\) km
Write the ratio and simplify. \(30 ∶ 36 ⇒ 5 ∶ 6\)

58- Choice D is correct
Use Pythagorean Theorem: \(a^2+b^2=c^2\)
\(12^2+16^2=c^2 ⇒ 144+256=c^2 ⇒ 400=c^2⇒c=20\)

59- Choice B is correct
The percent of girls playing tennis is: \(60\%×30\%=0.60×0.30=0.18=18\%\)

60- Choice B is correct
Let x be the number. Write the equation and solve for \(x\). \((30-x)÷x=4\),
Multiply both sides by \(x\).
\((30- x)=4x\), then add x both sides. \(30=5x\), now divide both sides by 5. \(x=6\)

61- Choice D is correct
The area of the floor is: \(9 \space cm × 25 \space cm = 225 \space cm^2\)
The number of tiles needed \(= 225 ÷ 5 = 45\)

62- Choices A is correct
The area of the circle is less than 16π. Use the formula of areas of circles.
Area\(=πr^2 ⇒ 16 π> πr^2⇒ 16> r^2⇒ r<4\)
The radius of the circle is less than 4. Let’s put 4 for the radius. Now, use the circumference formula:
Circumference\(=2πr=2π (4)=8π\)
Since the radius of the circle is less than 4. Then, the circumference of the circle must be less than \(8π\).
Only choice A is less than \(8π\).

63- Choice A is correct
Solving Systems of Equations by Elimination
\(\begin{cases}2x+3y=-7 \\x-2y=7\end{cases}\)
Multiply the second equation by \(-2\), then add it to the first equation.
\(\begin{cases}2x+3y= -7\\-2(x-2y=7)\end{cases}\)
⇒ \(\begin{cases}2x+3y= -7\\-2x+4y=-14\end{cases}\)
⇒ \(7y=-21 ⇒ y=-3\)

64- Choice C is correct
If the length of the box is 18, then the width of the box is one-third of it, 6, and the height of the box is 2 (one-third of the width). The volume of the box is: \(V=lwh=(18)(6)(2)=216\)
65- Choice D is correct
Write the equation and solve for B: \(0.75A=0.25B\), divide both sides by \(0.25\), then:
\(\frac{0.75}{0.25}A=B\), therefore: \(B=3A\), and \(B\) is 3 times of \(A\) or it’s \(300\%\) of \(A\).

66- Choice A is correct
To find the number of possible outfit combinations, multiply the number of options for each factor: \(4×5×3=60\)

67- Choice C is correct
Use simple interest formula: I = prt (I = interest, p = principal, r = rate, t = time)
\(I=(10,000)(0.030)(5)=1,500\)

68- Choice D is correct
Use percent formula: part\(=\frac{percent}{100}×whole\)
\(125=\frac{percent}{100}×50 ⇒ 125=\frac{percent ×50}{100} ⇒ 125= \frac{percent ×5}{10}\), multiply both sides by \(10\).
\(1,250=percent×5\), divide both sides by 5. \(250=percent\)

69- Choice B is correct
The perimeter of the trapezoid is 54.
Therefore, the missing side (height) is \(=46-14-9-11=12\)
Area of a trapezoid: \(A=\frac{1}{2} h (b_1+ b_2)=\frac{1}{2}(12)(9+11)=120\)

70- Choice D is correct
Add the first 5 numbers. 60 + 55 + 45 + 70 + 65 = 295
To find the distance traveled in the next 5 hours, multiply the average by number of hours.
Distance = Average × Rate = 65 × 5 = 325, Add both numbers. 325 + 295 = 620

Best TABE 11 & 12 Math Prep Resource for 2022

71- Choice C is correct
Use distance formula: Distance = Rate × time ⇒ \(360 = 48 × T\), divide both sides by 48. \(\frac{360}{48}= T\) ⇒ \(T = 7.5\) hours.
Change hours to minutes for the decimal part. 0.5 hours = 0.5 × 60 = 30 minutes.

72- Choice D is correct
Let x be the number. Write the equation and solve for \(x\).
\(\frac{2}{3}×24=\frac{2}{5}. x ⇒ \frac{2×24}{3}= \frac{2x}{5}\), use cross multiplication to solve for \(x\).
\(10×24=2x×3 ⇒240=6x ⇒ x=40\)

73- Choice C is correct
To find the discount, multiply the number by \((100\% – rate \space of \space discount)\).
Therefore, for the first discount we get: \((D) (100\% – 15\%) = (D) (0.85) = 0.85 D\)
For increase of \(8\%\): \((0.85 D) (100\% + 8\%) = (0.85 D) (1.08) = 0.918 D = 91.8\%\) of \(D\)

74- Choice C is correct
Use the formula for Percent of Change: \(\frac{New \space Value-Old \space Value}{Old \space Value}× 100\%\)
\(\frac{32-50}{50}× 100\% = –36\%\) (negative sign here means that the new price is less than old price).

75- Choice A is correct
The ratio of boys to girls is 3: 5. Therefore, there are 3 boys out of 8 students. To find the answer, first, divide the total number of students by 8, then multiply the result by 3.
400 ÷ 8 = 50 ⇒ 50 × 3 = 150

76- Choice B is correct
The question is this: 1.89 is what percent of 1.48?
Use percent formula: part \(= \frac{percent}{100} × whole\)
\(1.89 = \frac{percent}{100} × 1.48 ⇒ 1.89 = \frac{percent ×1.48}{100} ⇒189 = percent ×1.48 ⇒ percent = \frac{189}{1.48}= 127.7\)

77- Choice D is correct
The question is this: 514.5 is what percent of 735?
Use percent formula: part \(= \frac{percent}{100} × whole\)
\(514.5 = \frac{percent}{100}× 735 ⇒ 514.5 =\frac{percent ×735}{100} ⇒51,450 = percent ×735 ⇒\)
\(percent = \frac{51,450}{735} = 70\)
\(514.5\) is \(70 \%\) of \(735\). Therefore, the discount is: \(100\% – 70\% = 30\%\)

78- Choice A is correct
If the score of Mia was 50, therefore the score of Ava is 25. Since the score of Emma was half as that of Ava, therefore, the score of Emma is 12.5.

79- Choice C is correct
If 14 balls are removed from the bag at random, there will be one ball in the bag.
The probability of choosing a red ball is 1 out of 15. Therefore, the probability of not choosing a red ball is 14 out of 15 and the probability of having not a red ball after removing 14 balls is the same.

80- Choice D is correct
Let \(x\) be the smallest number. Then, these are the numbers:
\(x, x+1, x+2, x+3, x+4\)
average \(=\frac{sum \space of \space terms}{number \space of \space terms}\)⇒ \(47 = \frac{x+(x+1)+(x+2)+(x+3)+(x+4)}{5}\)⇒\(47=\frac{5x+10}{5} ⇒ 235 = 5x+10 ⇒225 = 5x ⇒ x=45\)

81- Choice C is correct
The equation of a line is in the form of \(y=mx+b\), where m is the slope of the line and \(b\) is the \(y\)-intercept of the line.
Two points (2, 3) and (1, 1) are on line A. Therefore, the slope of the line A is:
slope of line A\(=\frac{y_2- y_1}{x_2 – x_1}=\frac{1-3}{1-2} =\frac{-2}{-1}=2\)
The slope of line A is 2. Thus, the formula of line A is: \(y=mx+b=2x+b\), choose a point and plug in the values of \(x\) and \(y\) in the equation to solve for \(b\).
Let’s choose point (1, 1). Then: \(y=2x+b→1=2+b→b=1-2=-1\)
The equation of line A is: \(y=2x-1\)
Now, let’s review the choices provided:
A. \((1,2) →y=2x-1→2=2-1=1\) This is not true.
B. \((3,6) →y=2x-1→6=2(3)-1=5\) This is not true.
C. \((3,5) →y=2x-1→5=2(3)-1=5\) This is true !
D. \((1,-2) →y=2x-1→-2=2-1=1\) This is not true.

82- Choice C is correct
The weight of 15.5 meters of this rope is: 15.5 × 500 g = 7,750 g
1 kg = 1,000 g, therefore, 7,750 g ÷ 1000 = 7.75 kg

83- Choice C is correct
5% of the volume of the solution is alcohol. Let \(x\) be the volume of the solution.
Then: \(5\%\) of \(x = 45\) ml ⇒ \(0.05 x = 45 ⇒ x = 45 ÷ 0.05 = 900\)

84- Choice D is correct
average \(= \frac{sum \space of \space terms}{number \space of \space terms}\)
The sum of the weight of all girls is: 16 × 50 = 800 kg
The sum of the weight of all boys is: 24 × 65 = 1560 kg
The sum of the weight of all students is: 1560 + 800 = 2360 kg
average \(= \frac{2,360}{40} = 98.33\)

85- Choice C is correct
Let \(x\) be the original price. If the price of a laptop is decreased by \(20\%\) to $860, then:
\(80\%\) of \(x=860⇒ 0.80x=860 ⇒ x=860÷0.80=1,075\)

86- Choices C is correct
Some of the prime numbers are: 2, 3, 5, 7, 11, 13
Find the product of two consecutive prime numbers: 2 × 3 = 6 (not in the options)
3 × 5 = 15 (not in the options) 5 × 7 = 35 (bingo!) Choice C is correct.

87- Choice B is correct
Surface Area of a cylinder = 2πr (r + h),
The radius of the cylinder is 4 inches and its height is 10 inches. π is 3.14. Then:
Surface Area of a cylinder = 2 (3.14) (4) (4 + 10) = 351.68

88- Choice D is correct
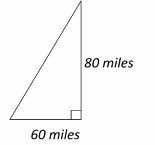
Use the information provided in the question to draw the shape.
Use Pythagorean Theorem: \(a^2 + b^2 = c^2\)
\(80^2 + 60^2 = c^2 ⇒ 6400 + 3600 = c^2 ⇒ 10,000 = c^2 ⇒ c = 100\)

89- Choice A is correct
Let \(x\) be the number of years. Therefore, $1,600 per year equals \(1,600x\).
starting from $18,000 annual salary means you should add that amount to \(1,600x\).
Income more than that is: \(I > 1,600x + 18,000\)

90- Choice A is correct
For each option, choose a point in the solution part and check it on both inequalities.
\(y≤x+4\)
\(2x+y≤-4\)
A. Point \((–4, –4)\) is in the solution section. Let’s check the point in both inequalities.
\(–4 ≤ – 4 + 4\), It works
\(2 (–4) + (–4) ≤ –4 ⇒ – 12 ≤ – 4,\) it works (this point works in both)
B. Let’s choose this point \((0, 0)\)
\(0 ≤ 0 + 4\), It works
\(2 (0) + (0) ≤ –4\), That’s not true!
C. Let’s choose this point \((–5, 0)\)
\(0 ≤ –5 + 4\), That’s not true!
D. Let’s choose this point \((0, 5)\)
\(5 ≤ 0 + 4\), That’s not true!

The Best Book to Ace the TABE Test

More from Effortless Math for TABE Test …

Do you need a study plan to better manage your time during studying TABE math content?

To have a better study plan, first read the Top 10 Tips to Create a TABE Math Study Plan.

Do you get anxious when you think about the TABE math test?

We know the solution to this concern: Top 10 Tips to Overcome TABE Math Anxiety

Did not find the TABE practice math test you are looking for?

You will find what you are looking for here: FREE TABE Math Practice Test.

The Perfect Prep Books for the TABE Math Test

Have any questions about the TABE Test?

Write your questions about the TABE or any other topics below and we’ll reply!