10 Most Common TSI Math Questions

Preparing for the TSI Math test? Want a preview of the most common mathematics questions on the TSI Math test? If so, then you are in the right place.

The mathematics section of TSI can be a challenging area for many test-takers, but with enough patience, it can be easy and even enjoyable!

Preparing for the TSI Math test can be a nerve-wracking experience. Learning more about what you’re going to see when you take the TSI can help to reduce those pre-test jitters. Here’s your chance to review the 10 most common TSI Math questions to help you know what to expect and what to practice most. Try these 10 most common TSI Math questions to hone your mathematical skills and to see if your math skills are up to date on what’s being asked on the exam or if you still need more practice.

Make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions you need to practice.

The Absolute Best Book to Ace the TSI Math Test

10 Sample TSI Math Practice Questions

1- If \(f(x) = 5 + x\) and \(g(x) = – x^2 – 1 – 2x\), then find \((g – f)(x)\)?

A. \(x^2 – 3x – 6\)

B. \(x^2 – 3x +6\)

C. \(-x^2 – 3x +6\)

D. \(-x^2 – 3x – 6\)

2- \(\frac{|3+x|}{7}≤ 5, then \space x = ?\)

A. \(–38 ≤ x ≤ 35\)

B. \(–38 ≤ x ≤ 32\)

C. \(–32 ≤ x ≤ 38\)

D. \(–32 ≤ x ≤ 32\)

3- \(tan\space (-\frac{π}{6}) = ?\)

A. \(\frac{{\sqrt{3}}}{3}\)

B. \(-\frac{{\sqrt{2}}}{2}\)

C. \(\frac{{\sqrt{2}}}{2}\)

D. \(-\frac{{\sqrt{3}}}{3}\)

4- \(\frac{\sqrt {32a^5 b^3} }{\sqrt {2ab^2} }= ?\)

A. \(4a^2 {\sqrt{b}}\)

B. \(2b^2 {\sqrt{a}}\)

C. \(4b^2 {\sqrt{a}}\)

D. \(-4a^2 {\sqrt{b}}\)

5- The cost, in thousands of dollars, of producing x thousands of textbooks is \(C (x) = x2 + 10x + 30\). The revenue, also in thousands of dollars, is \(R(x) = 4x\). Find the profit or loss if 3,000 textbooks are produced. \((profit = revenue – cost)\)

A. $21,000 loss

B. $57,000 profit

C. $3,000 profit

D. $57,000 loss

6- Suppose \(a\) triangle has the dimensions indicated below:
Then\(Sin B =\) ?

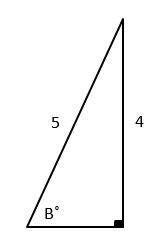
A. \(\frac{3}{5}\)

B. \(\frac{4}{5}\)

C. \(\frac{4}{3}\)

D. \(\frac{3}{4}\)

7- Find the slope-intercept form of the graph \(6x – 7y = – 12\)

A. \(y = –\frac{7}{6} x – \frac{12}{7}\)

B. \(y = –\frac{6}{7} x – \frac{12}{7}\)

C. \(y = \frac{6}{7} x +\frac{12}{7}\)

D. \(y = \frac{7}{6} x +\frac{12}{7}\)

8- Ella (E) is 4 years older than her friend Ava (A) who is 3 years younger than her sister Sofia (S). If E, A, and S denote their ages, which one of the following represents the given information?

A.
\(E=A+4\)
\(S=A-3\)

B.
\(E=A+4\)
\(A=S+3\)

C.
\(A=E+4\)
\(S=A-3\)

D.
\(E=A+4\)
\(A=S-3\)

9- Which of the following point is the solution of the system of equations?
\(5x + y = 9 \)
\(10x-7y= -18\)

A. \((2, 4)\)

B. \((2, 2)\)

C. \((1, 4)\)

D. \((0, 4)\)

10- Find the Center and Radius of the graph \((x – 3)^2 + (y + 6)^2 = 12\)

A. \((3, 6), \sqrt{3}\)

B. \((3, -6), 2\sqrt{3}\)

C. \((-3, 6), 2\sqrt{3}\)

D. \((3, -6), \sqrt{3}\)

Best TSI Math Prep Resource for 2022

Answers:

2- B
\(\frac{|3+x|}{7}≤ 5⇒|3+x|≤35⇒-35≤3+x≤35⇒-35-3≤x≤35-3⇒
-38≤x≤32\)

3- D
\(tan\space (-\frac{π}{6}) = -\frac{\sqrt3}{3}\)

4- A
\(\frac{\sqrt{32a^5 b^3} }{\sqrt{2ab^2} }=\frac{4a^2 b\sqrt{2ab}}{b\sqrt{2a}}=4a^2 \sqrt b\)

5- D
\(c(3)=(3)^2+10(3)+30=9+30+30=69\)
\(4×3=12⇒12-69=-57⇒57,000 \space loss\)

6- B
\(sin\space B=\frac{the \space length \space of \space the \space side \space that \space is \space opposite \space that \space angle}{the \space length \space of \space the \space longest \space side \space of \space the \space triangle}=\frac{4}{5}\)

7- C
\(-7y=-6x-12⇒y=\frac{-6}{-7}x- \frac{12}{-7}⇒y=\frac{6}{7}x + \frac{12}{7}\)

8- D
\( E = 4 + A\)
\(A = S – 3\)

9- C
\(5x + y = 9 \)
\(10x-7y= -18\)
Multiplication \((–2)\) in the first equation
\(-10x- 2y = -18 \)
\(10x-7y= -18\)
Add two equations together \(⇒ –9y = –36 ⇒ y = 4\) then: \(x = 1\)

10- B
\((x – h)^2 + (y – k)^2 = r^2\) ⇒ center: (h,k) and radius: \(r\)
\((x – 3)^2 + (y + 6)^2 = 12\) ⇒ center: \((3,-6)\) and radius:\(2\sqrt 3\)

Looking for the best resource to help you succeed on the TSI Math test?

The Best Book to Ace the TSI Math Test

More from Effortless Math for TSI Test …

Looking for an article that explains well the TSI math test for you?

We know your needs and have prepared an Overview of the TSI Mathematics Test to meet that need

Have not yet found the math worksheets necessary to practice TSI?

You can use TSI Math Worksheets: FREE & Printable to get the best test results.

How familiar are you with the TSI math test scoring method?

How is the TSI Test Scored help you become more familiar with the TSI test scores section.

The Perfect Prep Books for the TSI Math Test

Have any questions about the TSI Test?

Write your questions about the TSI or any other topics below and we’ll reply!