How to graph Scatter Plots? (+FREE Worksheet!)
On a scatter plot, you can use a trend line to make predictions. The scatter of points from the trend line shows how well the data has performed in the predicted pattern.
A scatter plot shows a positive trend if \(y\) tends to increase as \(x\) increases.
A scatter plot shows a negative trend if \(y\) tends to decrease as \(x\) increases.
An outlier is an extreme point in a data set that is separated from all other points.
Scatter Plots – Example 1:
The following table shows the number of people in a family and the amount of money they spend on movie tickets.
| Number of people | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Money ($) | 15 | 18 | 20 | 37 | 23 | 23 | 27 | 28 |
a) Make a scatter plot to represent the data.
b) Does this scatter plot show a positive trend, a negative trend, or no trend?
c) Find the outlier on the scatter plot.
Solution:
a) Write the ordered pairs. The number of people goes on the \(x\)-axis, so put the number of people first. The amount of money goes on the \(y\)-axis, so put the amount of money second.\((1, 15), (2, 18), (3, 20), (4, 37), (5, 23), (6, 23), (7, 27), (8, 28)\). Now, graph the ordered pairs.
b) \(y\) tends to increase as \(x\) increases. So, this scatter plot shows a positive trend.
c) \( (4, 37)\) is the outlier because this point is separated from all other points in the data set.
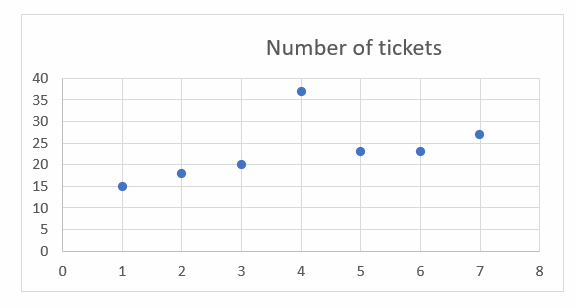
Scatter Plots – Example 2:
The table below shows the number of students on a basketball team and the number of free throws each student made during practice.
| student | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Free throws | 9 | 9 | 10 | 11 | 12 | 1 | 12 | 14 | 15 | 17 |
a) Make a scatter plot to represent the data.
b) Does this scatter plot show a positive trend, a negative trend, or no trend?
C)Find the outlier on the scatter plot.
Solution:
a) Write the ordered pairs. The number of students goes on the \(x\)-axis, so put the number of people first. The number of free throws goes on the \(y\)-axis, so put the number of free throws second.\((1, 9), (2, 9), (3, 10), (4, 11), (5, 12), (6, 1), (7, 12), (8, 14), (9, 15), (10, 17)\). Now, graph the ordered pairs.
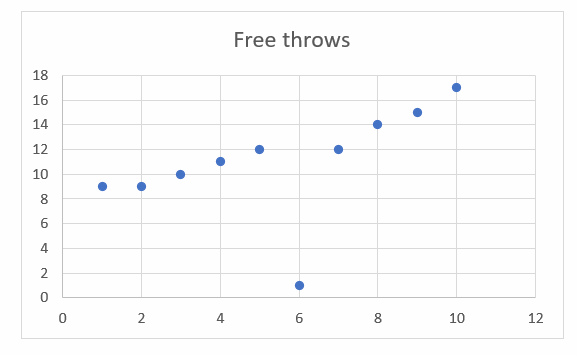
b)\(y\) tends to increase as \(x\) increases. So, this scatter plot shows a positive trend.
C) \( (6, 1)\) is the outlier because this point is separated from all other points in the data set.
Exercises for graphing Scatter Plots
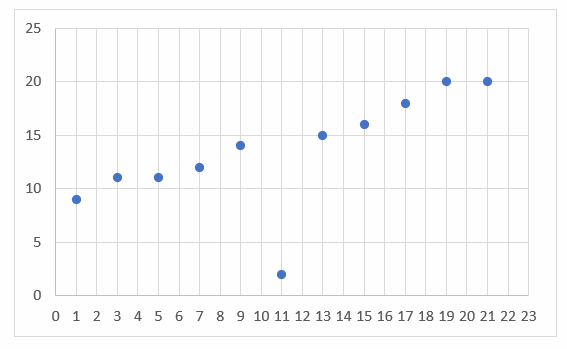
Use the given data to make a scatter plot. Does this scatter plot represent a positive trend, a negative trend, or no trend? Find the outlier on the scatter plot.
| x | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 |
| y | 9 | 11 | 11 | 12 | 14 | 2 | 15 | 16 | 18 | 20 | 20 |
First, find the ordered pairs.\((1, 9), (3, 11), (5, 11), (7, 12), (9, 14), (11, 2), (13, 15), (15, 16), (17, 18), (19, 20), (21, 20)\). Now, graph the ordered pairs. \(y\) tends to increase as \(x\) increases. So, this scatter plot represents a positive trend. An outlier is a point that is separated from all other points. So, point \((11, 2)\) is the outlier.
Related to This Article
More math articles
- Top 10 Praxis Core Math Practice Questions
- What Kind of Math Is on the AFOQT Test?
- ISEE Middle-Level Math Worksheets: FREE & Printable
- The Ultimate PERT Math Course (+FREE Worksheets & Tests)
- The Ultimate Adults Math Refresher Course (+FREE Worksheets & Tests)
- How to Find the Area of Composite Shapes?
- 3rd Grade CMAS Math Worksheets: FREE & Printable
- How to Write the Standard Form of Linear Equations?
- 7th Grade ACT Aspire Math Worksheets: FREE & Printable
- 7 Best PSAT Math Study Guides
What people say about "How to graph Scatter Plots? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.