10 Most Common CLEP College Algebra Math Questions

Preparing for the CLEP College Algebra Math test? Want a preview of the most common mathematics questions on the CLEP College Algebra Math test? If so, then you are in the right place.

The mathematics section of CLEP College Algebra can be a challenging area for many test-takers, but with enough patience, it can be easy and even enjoyable!

Preparing for the CLEP College Algebra Math test can be a nerve-wracking experience. Learning more about what you’re going to see when you take the CLEP College Algebra can help to reduce those pre-test jitters. Here’s your chance to review the 10 most common CLEP College Algebra Math questions to help you know what to expect and what to practice most. Try these 10 most common CLEP College Algebra Math questions to hone your mathematical skills and to see if your math skills are up to date on what’s being asked on the exam or if you still need more practice.

Make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions you need to practice.

The Absolute Best Book to Ace the CLEP College Algebra Math Test

10 Sample CLEP College Algebra Math Practice Questions

1- The marked price of a computer is D dollar. Its price decreased by \(25%\) in January and later increased by \(10%\) in February. What is the final price of the computer in D dollars?

A. 0.80 D

B. 0.82 D

C. 0.90 D

D. 1.20 D

E. 1.40 D

2- If A={2,5,11,15}, B={1,2,3,4,5,6}, and C={5,7,9,11,13}, then which of the following set is \((A∪B)∩C\)?

A. {1,2,3,4,5,6,11,15}

B. {1,2,3,4,5,6,7,11,13,15}

C. {5,11,13,15}

D. {5,11}

E. {11}

3- The average of 13,15,20 and \(x\) is 20. What is the value of \(x\)?

A. 9

B. 15

C. 18

D. 20

E. 32

4- What is the ratio of the minimum value to the maximum value of the following function?
\(f(x)=-3x+1 \)
\(-2≤x≤3\)

A. \(\frac{7}{8}\)

B. \(-\frac{8}{7}\)

C. \(-\frac{7}{8}\)

D. \(\frac{8}{7}\)

E. \(\frac{6}{7}\)

5- The equation \(x^2=4x-3\) has how many distinct real solutions?

A. 0

B. 1

C. 2

D. 3

E. 4

6- For what value of \(x\) is \(|x-3|+3\) equal to 0?

A. 1

B. 2

C. no value of \(x\)

D. \(-3)\

E. 3

7- In 1999, the average worker’s income increased by $2,000 per year starting from $26,000 annual salary. Which equation represents income greater than average? (I= income, \(x \)= number of years after 1999)

A. \( I > 2000 x +26000\)

B. \( I >-2000 x +26000\)

C. \( I <-2000 x + 26000\)

D. \( I < 2000 x-26000\)

E. \( I < 24,000 x+26000\)

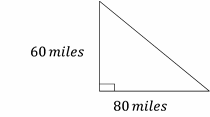
8- A boat sails 60 miles south and then 80 miles east. How far is the boat from its start point?

A. 45 miles

B. 50 miles

C. 60 miles

D. 70 miles

E. 100 miles

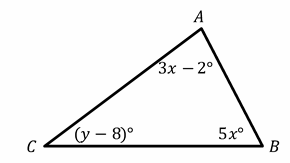
9-In the triangle below, if the measure of angle A is 37 degrees, then what is the value of y? (the figure is NOT drawn to scale)

A. 70

B. 78

C. 84

D. 86

E. 92

10- The score of Emma was half as that of Ava and the score of Mia was twice that of Ava. If the score of Mia was 40, what is the score, Emma?

A. 10

B. 15

C. 20

D. 30

E. 40

Best CLEP College Algebra Math Prep Resource for 2024

Answers:

2- D
The union of A and B is: \(A∪B\) = {1,2,3,4,5,6,11,15}
The intersection of \((A∪B)\) and C is: \((A∪B)∩C\)={5,11}

3- E
average\(=\frac{sum \ of \ terms}{number \ of \ terms} ⇒20=\frac{13+15+20+x}{4}⇒80=48+x ⇒ x=32\)

4- B
Since \(f(x)\) is linear function with a negative slop, then when \(x=-2,f(x)\) is maximum and when \(x=3,f(x)\) is minimum. Then the ratio of the minimum value to the maximum value of the function is: \(\frac{f(3)}{f(-2)}=\frac{-3(3)+1}{-3(-2)+1}=\frac{-8}{7}=-\frac{8}{7}\)

5- C
There can be 0, 1, or 2 solutions to a quadratic equation. In standard form, a quadratic equation is written as: \(ax^2+bx+c=0\)
For the quadratic equation, the phrase \(b^2-4ac\) is called the discriminant. If the discriminant is positive, there are 2 distinct solutions for the quadratic equation. If the discriminant is 0, there is one solution for the quadratic equation and if it is negative the equation does not have any solutions.
To find number of solutions for \(x^2=4x-3\), first, rewrite it as \(x^2-4x+3=0\).
Find the value of the discriminant. \(b^2-4ac=(-4)^2-4(1)(3)=16-12=4\)
Since the discriminant is positive, the quadratic equation has two distinct solutions.

6- C
If the value of \(|x-3|+3\) is equal to 0, then \(|x-3|+3=0\). Subtracting 3 from both sides of this equation gives \(|x-3|\)=\(-3\). The expression \(|x – 3|\) on the left side of the equation is the absolute value of \(x \)\(- 3\), and the absolute value can never be a negative number.
Thus \(|x-3|\)=\(-3\) has no solution. Therefore, there are no values for \(x\) for which the value of \(|x(-3)|+3\) is equal to 0.

7- A
Let \(x\) be the number of years. Therefore, $2,000 per year equals 2000\(x\). starting from $26,000 annual salary means you should add that amount to 2000\(x\). Income more than that is:
\(I>2000 x + 26000\)

8- E
Use the information provided in the question to draw the shape.
Use Pythagorean Theorem: \(a^2+b^2=c^2\)
\(60^2+80^2= c^2⇒ 3600 +6400 =c^2 ⇒ 10000 =c^2 ⇒ c=100\)

9- D
In the figure angle A is labeled \((3x-2)\) and it measures 37. Thus, 3\(x\)\(-2\)=37 and 3\(x\)=39 or \(x\)=13. That means that angle B, which is labeled \((5x)\), must measure 5×13=65.
Since the three angles of a triangle must add up to 180, 37+65+y\(-8\)=180, then:
y+94=108→y=180\(-94\)=86

10- A
If the score of Mia was 40, therefore the score of Ava is 20. Since the score of Emma was half as that of Ava, therefore, the score of Emma is 10.

Looking for the best resource to help you succeed on the CLEP College Algebra Math test?

The Best Books to Ace the CLEP College Algebra Math Test