How to Solve Pascal’s Triangle?

TL;DR: Pascal's Triangle is one of those things that looks like a puzzle but turns out to be a Swiss Army knife. Each entry is just the sum of the two above it. From that tiny rule come the coefficients you need to expand any (a + b) to a power, the counts you need for combinatorics problems, the probabilities you need for coin flips, even Fibonacci numbers, hiding along a diagonal.

Quick answer: Pascal's triangle is a triangle of numbers where every row starts and ends with 1 and each inside number is the sum of the two numbers above it. Row n lists the values C(n, k) = n!/(k!(n − k)!). Example: row 4 is 1, 4, 6, 4, 1, so (a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴.

Key takeaways:

Each row starts and ends with 1.
Every other entry is the sum of the two numbers directly above it.
Row n (counting from 0) contains the binomial coefficients C(n, 0), C(n, 1).., C(n, n).
The numbers expand (a + b)^n directly: (a+b)^4 = a^4 + 4a^3 b + 6a^2 b^2 + 4ab^3 + b^4.
Sum of row n equals 2^n.

Pascal’s triangle is an arrangement of numbers in a triangular array. In this post, you will learn more about Pascal’s Triangle.

Tutor-style math help

Solve Pascal’s Triangle: what to notice and how to work it

Series skill

Sequences list terms; series add terms. The first question is whether the pattern adds the same amount or multiplies by the same factor.

What to notice first

Identify the term number. Many mistakes happen because \(a_1\), \(a_n\), and the number of terms get mixed up.

Common student mistake

Do not use an arithmetic formula on a geometric pattern. Check differences and ratios before choosing a formula.

Key formulas and cues

\(a_n=a_1+(n-1)d\)

\(a_n=a_1r^{n-1}\)

\(S_n=\frac{n}{2}(a_1+a_n)\)

\(S_n=a_1\frac{1-r^n}{1-r}\)

A reliable path

Compare termsLook for a common difference or common ratio.
Choose term or sumDecide whether the question asks for one term or a total.
Track nMake sure n is the position or number of terms the question uses.

Worked examples

Arithmetic sequence

Example: 5, 9, 13, 17..

Each term adds 4.
The common difference is 4.
Add 4 to continue.

Answer: \(21\)

Geometric sequence

Example: 3, 6, 12, 24..

Each term multiplies by 2.
The common ratio is 2.
Multiply 24 by 2.

Answer: \(48\)

Open pop-up practice

Try one before moving on

Try: Find the next term: 10, 7, 4, 1..

Answer: \(-2\). The pattern subtracts 3.

Next step: do the matching worksheet or quiz while the method is still fresh, then come back and explain the first step in your own words.

Pascal’s triangle can be used for many purposes in mathematics. It is used in probability, to find the number of combinations, in the binomial expansion of a polynomial, and can be used to find the Fibonacci series.

A step-by-step guide to Pascal’s triangle

Pascal’s triangle is an arrangement of numbers in a triangular array such that the numbers at the end of each row are \(1\) and the remaining numbers are the sum of the two nearest numbers in the row above. The number of elements in the \(nth\) row is equal to \((n + 1)\) elements.

Pascal’s triangle can be easily constructed by adding the pairs of consecutive numbers in the previous lines and writing them in the new line.

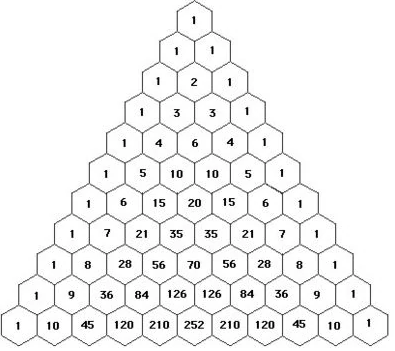
we use Pascal’s triangle formula to fill the number in the \(nth\) column and \(mth\) row of Pascal’s triangle. The formula requires the knowledge of the elements in the \(\left(n-1\right)^{th}\) row, and \(\left(m-1\right)^{th}\) and \(m^{th}\) columns. The elements of the \(n^{th}\) row of Pascal’s triangle are given by, \(^nC_0\), \(^nC_1\), \(^nC_2\), …, \(^nC_n\). The formula for Pascal’s triangle is:

\(\color{blue}{^nC_m\:=\:^{n-1}C_{m-1}+\:^{n-1}C_{m}}\)

where

\(^nC_m\) shows the \(\left(m+1\right)^{th}\) element in the \(n^{th}\) row.
\(n\) is a non-negative integer
\(0≤ m≤n\).

Geometry for Beginners The Ultimate Step by Step Guide to Acing Geometry

Pascal’s triangle pattern

Pascal’s triangle has various patterns within the triangle that were discovered and explained by Pascal himself or known before him. Some of Pascal’s triangle patterns are:

The sum of values in the \(n^{th}\) row is \(2^n\).
If a row has a second element that is a prime, then all the numbers in the row except the 1s at each end are divisible by that prime (not including (1s)). Ex. \(1 5 10 10 5 1\).
By adding the numbers along each shallow diagonal of Pascal’s triangle, we get the Fibonacci series.

Pascal’s Triangle, Example 1:

Find the \(3rd\) element in the \(4th\) row.

Solution:

This means you want to calculate \(^4C_2\:\). Then according to the formula:

\(^4C_2\:=^{4-1}C_{2-1}+^{4-1}C_2\:\:\)

\(^4C_2=^3C_1+^3C_2\)

So, this means we need to add the \(2nd\) element in the \(3rd\) row (i.e. \(3\)) with the \(3rd\) element in the \(3rd\) row (i.e. \(3\).). So that would be our answer:

\(^4C_2=3+3=6\)

Exercises for Pascal’s Triangle

Solve.

Write the \(6th\) row of Pascal’s Triangle.
What is the sum of the \(12th\) row of Pascal’s triangle?

\(\color{blue}{1, 6, 15, 20, 15, 6, 1}\)
\(\color{blue}{4096}\)

Pascal’s Triangle Rows 0 to 10

Rows are counted from 0. The row number is also the second number in each row.

Row	Numbers	Row sum
0	1	1
1	1 1	2
2	1 2 1	4
3	1 3 3 1	8
4	1 4 6 4 1	16
5	1 5 10 10 5 1	32
6	1 6 15 20 15 6 1	64
7	1 7 21 35 35 21 7 1	128
8	1 8 28 56 70 56 28 8 1	256
9	1 9 36 84 126 126 84 36 9 1	512
10	1 10 45 120 210 252 210 120 45 10 1	1024

A quick way to write any row

You don’t need the rows above it. Start with 1, then multiply by a fraction that changes each step: the top counts down from n and the bottom counts up from 1.

Example, row 5: 1 × 5/1 = 5, then 5 × 4/2 = 10, then 10 × 3/3 = 10, then 10 × 2/4 = 5, then 5 × 1/5 = 1. So row 5 is 1, 5, 10, 10, 5, 1.

Patterns Hidden in Pascal’s Triangle

Symmetry: each row reads the same forward and backward.
Diagonals: the first diagonal is all 1s, the second is the counting numbers 1, 2, 3, 4, and the third is the triangular numbers 1, 3, 6, 10, 15.
Powers of 2: the numbers in row n add up to 2ⁿ.
Powers of 11: rows 0 to 4 read as 1, 11, 121, 1331, 14641, which are 11⁰ to 11⁴. From row 5 on you carry digits: 1, 5, 10, 10, 5, 1 becomes 161051, which is 11⁵.
Fibonacci numbers: add the numbers along each shallow diagonal (going up and to the right at a slant). The sums are 1, 1, 2, 3, 5, 8, 13, and so on. For example, 1 + 3 + 1 = 5 and 1 + 4 + 3 = 8.
Odd and even: color the odd numbers and a pattern of triangles inside triangles appears, called the Sierpinski triangle.

Frequently Asked Questions

What is Pascal’s triangle used for?

Pascal’s triangle is used to find binomial coefficients, which give the numbers in expansions like (a + b)⁴. It also counts combinations, such as how many ways to choose 2 items from 5 (row 5 gives 10), and it helps with coin-flip probabilities. Patterns like powers of 2 and Fibonacci numbers also appear in it.

What is Pascal’s triangle formula?

Each entry is a combination: the number in row n, position k (both counting from 0) is C(n, k) = n!/(k!(n − k)!). For row 5, position 2, C(5, 2) = 120/(2 × 6) = 10. You can also build any row from the one above, since each inside number equals the sum of the two numbers above it.

How do you use Pascal’s triangle for binomial expansion?

Pick the row that matches the power, then use its numbers as coefficients. For (a + b)⁵, row 5 is 1, 5, 10, 10, 5, 1, so (a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵. The power of a drops by 1 in each term while the power of b rises by 1.

How do you make Pascal’s triangle?

Write 1 at the top as row 0, then 1 and 1 below it. Every new row starts and ends with 1, and each number in between is the sum of the two numbers just above it. Row 3 is 1, 3, 3, 1, so row 4 is 1, 1 + 3, 3 + 3, 3 + 1, 1, or 1, 4, 6, 4, 1.

How do you use Pascal’s triangle for probability?

For fair coin flips, row n lists how many ways each number of heads can happen out of 2ⁿ outcomes. With 4 flips, row 4 is 1, 4, 6, 4, 1, which totals 16. So the chance of exactly 2 heads is 6/16 = 3/8, and the chance of all heads is 1/16.

Is Pascal’s triangle powers of 11?

Partly. Reading rows 0 to 4 as numbers gives 1, 11, 121, 1,331 and 14,641, which are 11⁰ through 11⁴. From row 5 on, entries have two digits, so you must carry: 1, 5, 10, 10, 5, 1 becomes 161,051, which is 11⁵. Without carrying, the pattern breaks.

Is Pascal’s triangle related to the Fibonacci sequence?

Yes. If you add the numbers along the shallow diagonals of Pascal’s triangle, the sums are the Fibonacci numbers 1, 1, 2, 3, 5, 8, 13 and so on. For example, the diagonal through 1, 3 and 1 adds to 5, and the next one through 1, 4 and 3 adds to 8.

What is the formula for the nth row of Pascal’s triangle?

The kth number in row n (counting both from 0) is C(n, k) = n!/(k!(n − k)!). So row n is C(n, 0), C(n, 1), and so on up to C(n, n). For row 6 that gives 1, 6, 15, 20, 15, 6, 1. Each entry can also be found from the one before it by multiplying by (n − k)/(k + 1).

How do you find a number in Pascal’s triangle without drawing it?

Use the combination formula. To find the number in row 8, position 3 (counting from 0), compute C(8, 3) = 8!/(3! × 5!) = (8 × 7 × 6)/(3 × 2 × 1) = 56. Check it in the table: row 8 is 1, 8, 28, 56, 70, 56, 28, 8, 1.

Why is it called Pascal’s triangle?

It is named after the French mathematician Blaise Pascal, who wrote a well-known treatise on it in the 1600s. The pattern was known much earlier, though. Mathematicians in China, Persia and India studied it centuries before Pascal, and in China it is often called Yang Hui’s triangle.

Related Lessons You May Like

For deeper combinatorics and the binomial theorem, Algebra II for Beginners covers expansion and counting techniques. Pre-Calculus for Beginners extends into sequences and series.

Effortless Math Team

1 week ago

Effortless Math Team

Related to This Article

Pascal’s Triangle

What people say about "Pascal's Triangle: Rows, Formula, Patterns & Examples"?

No one replied yet.

How to Solve Pascal’s Triangle?