How to Solve One-Step Inequalities? (+FREE Worksheet!)
To solve one-step inequalities, you only need to do one math operation. Learn how to solve one-step inequalities easily.
[include_netrun_products_block from-products="product/the-most-comprehensive-ftce-math-preparation-bundle-includes-ftce-math-prep-books-workbooks-and-practice-tests/" product-list-class="bundle-products float-left" product-item-class="float-left" product-item-image-container-class="p-0 float-left" product-item-image-container-size="col-2" product-item-image-container-custom-style="" product-item-container-size="" product-item-add-to-cart-class="btn-accent btn-purchase-ajax" product-item-button-custom-url="{{url}}/?ajax-add-to-cart={{id}}" product-item-button-custom-url-if-not-salable="{{productUrl}} product-item-container-class="" product-item-element-order="image,title,purchase,price" product-item-title-size="" product-item-title-wrapper-size="col-10" product-item-title-tag="h3" product-item-title-class="mt-0" product-item-title-wrapper-class="float-left pr-0" product-item-price-size="" product-item-purchase-size="" product-item-purchase-wrapper-size="" product-item-price-wrapper-class="pr-0 float-left" product-item-price-wrapper-size="col-10" product-item-read-more-text="" product-item-add-to-cart-text="" product-item-add-to-cart-custom-attribute="title='Purchase this book with single click'" product-item-thumbnail-size="290-380" show-details="false" show-excerpt="false" paginate="false" lazy-load="true"]
Watch this practice video for additional examples and reinforcement:
Related Topics
- How to Solve One-Step Equations
- How to Solve Multi-Step Equations
- How to Solve Multi-Step Inequalities
- How to Solve Systems of Equations
- How to Graph Single–Variable Inequalities
Step by step guide to solve one-step inequalities
- Similar to equations, first isolate the variable by using the inverse operation.
- For dividing or multiplying both sides by negative numbers, flip the direction of the inequality sign.
For education statistics and research National Center for Education Statistics.
The Absolute Best Books to Ace Pre-Algebra to Algebra II
One–Step Inequalities – Example 1:
Solve and graph the inequality. \(x \ + \ 2 \ ≥ \ 3\)
Solution:
Subtract \(2\) from both sides. \(x \ + \ 2 \ ≥ \ 3→x \ + \ 2 \ – \ 2 \ ≥ \ 3 \ – \ 2\), then: \(x \ ≥ \ 1\)
One–Step Inequalities – Example 2:
Solve and graph the inequality. \(x \ – \ 1 \ \leq \ 2\)
Solution:
Add \(1\) to both sides. \(x \ − \ 1 \ ≤ \ 2→x \ − \ 1 \ + \ 1 \ ≤ \ 2 \ + \ 1\), then: \(x \ ≤ \ 3\)
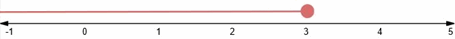
One–Step Inequalities – Example 3:
Solve and graph the inequality. \(x+5≥6\).
Solution:
Subtract \(5\) from both sides. \(x+5≥6→x+5-5≥6-5\), then: \(x≥1\)
One–Step Inequalities – Example 4:
Solve this inequality. \(x-6≤-3\)
Solution:
Add \(6\) to both sides. \(x-6≤-3→x-6+6≤-3+6\), then: \(x≤3\)
Exercises for Solving One–Step Inequalities
Solve each inequality and graph it.
1- \(\color{blue}{x + 9 ≥ 11}\)
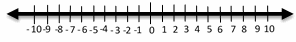
2- \(\color{blue}{x – 4 ≤ 2}\)
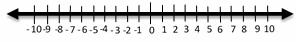
3- \(\color{blue}{6x ≥ 36}\)
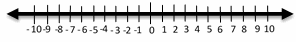
4- \(\color{blue}{7 + x < 16}\)
5- \(\color{blue}{x + 8 ≤ 1}\)
6- \(\color{blue}{3x > 12}\)
Download One-Step Inequalities Worksheet
Answers
The Greatest Books for Students to Ace the Algebra
Related to This Article
More math articles
- 6th Grade RICAS Math Worksheets: FREE & Printable
- The Fascinating Applications of Algebraic Manipulation in Limits
- HL Congruence: The Special Case of Right Triangles
- 10 Most Common ATI TEAS 7 Math Questions
- Decoding The Ding Ding Ding: How Math Can Unlock The Secrets Of Slot Machine
- Top 10 7th Grade PSSA Math Practice Questions
- How to Decipher Patterns: A Comprehensive Guide to Understanding Mathematical Sequences
- Full-Length 6th Grade SBAC Math Practice Test
- How to Understand and Master Polygons and Angles
- The Ultimate PERT Math Formula Cheat Sheet
What people say about "How to Solve One-Step Inequalities? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.