6th Grade MAP Math Practice Test Questions
6th Grade students, in order to further prepare for the 6th Grade MAP Math exams, should refer to the practice test questions. in addition, they should be familiar with the type of 6th Grade MAP Math questions and their variety, as well as the types of solutions for each of the questions in this exam.
Taking all kinds of 6th Grade MAP Math practice test questions will make your student familiar with the difficulty and ease of the questions in this test and will also reduce your student’s anxiety and worries.
Therefore, in this article, we have prepared 10 common 6th Grade MAP Math practice problems along with their exact and step-by-step solutions for your student’s further preparation.
The Absolute Best Book to Ace 6th Grade MAP Math Test
Common Core Math Exercise Book for Grade 6 Student Workbook and Two Realistic Common Core Math Tests
10 Sample 6th Grade MAP Math Practice Questions
1- What is the missing prime factor of number 420?
\(420=2^2×3^1×…\)
A. \(2^2×3^1×5^1×7^1\)
B. \(2^2×3^1×7^1×9^1\)
C. \(1^2×2^3×2^1×3^1\)
D. \(3^2×5^1×7^1×9^1\)
2- If the area of the following trapezoid is equal to \(A\), which equation represents \(x\)?
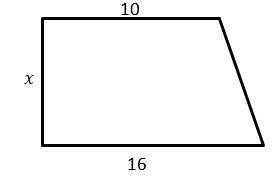
A. \( x = \frac{13}{A}\)
B. \( x = \frac{A}{13}\)
C. \( x=A+13\)
D. \( x=A-13\)
3- By what factor did the number below change from the first to the fourth number?
\(8, 104, 1352, 17576\)
A. 13
B. 96
C. 1456
D. 17568
4- 170 is equal to …
A. \( -20-(3×10)+(6×40)\)
B. \(((\frac{15}{8})×72 )+ (\frac{125}{5}) \)
C. \(((\frac{30}{4} + \frac{15}{2})×8) – \frac{11}{2} + \frac{222}{4}\)
D. \(\frac{481}{6} + \frac{121}{3}+50\)
5- The distance between the two cities is 3,768 feet. What is the distance between the two cities in yards?
A. 1,256 yd
B. 11,304 yd
C. 45,216 yd
D. 3,768 yd
6- Mr. Jones saves $3,400 out of his monthly family income of $74,800. What fractional part of his income does Mr. Jones save?
A. \(\frac{1}{22}\)
B. \(\frac{1}{11}\)
C. \(\frac{3}{25}\)
D. \(\frac{2}{15}\)
7- What is the lowest common multiple of 12 and 20?
A. 60
B. 40
C. 20
D. 12
8- Based on the table below, which expression represents any value of f in term of its corresponding value of \(x\)?
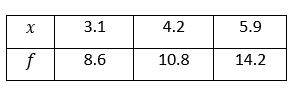
A. \(f=2x-\frac{3}{10}\)
B. \(f=x+\frac{3}{10}\)
C. \(f=2x+2 \frac{2}{5}\)
D. \(2x+\frac{3}{10}\)
9- 96 kg \(=\)… ?
A. 96 mg
B. 9,600 mg
C. 960,000 mg
D. 96,000,000 mg
10- Calculate the approximate area of the following circle? (the diameter is 25)
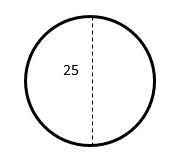
A. 78
B. 491
C. 157
D. 1963
Best 6th Grade MAP Math Prep Resource for 2022
Answers:
1- A
\(420=2^2×3^1×5^1×7^1\)
2- B
The area of the trapezoid is: area= \(\frac{(base 1+base 2)}{2})×height= ((\frac{10 + 16}{2})x = A\)
\( →13x = A→x = \frac{A}{13}\)
3- A
\(\frac{104}{8}=13, \frac{1352}{104}=13, \frac{17576}{1352}=13\)
Therefore, the factor is 13
4- C
Simplify each option provided.
\( A. -20-(3×10)+(6×40)=-20-30+240=190\)
\( B. (\frac{15}{8})×72 + (\frac{125}{5}) =135+25=160\)
\(C. ((\frac{30}{4} + \frac{15}{2})×8) – \frac{11}{2} + \frac{222}{4} = ((\frac{30 + 30}{4})×8)- \frac{11}{2}+ \frac{111}{2}=(\frac{60}{4})×8) + \frac{100}{2}= 120 + 50 = 170\)this is the answer
\(D. \frac{481}{6} + \frac{121}{3}+50= \frac{481+242}{6}+50=120.5+50=170.5\)
5- A
1 yard \(= \)3 feet
Therefore, \(3,768 ft × \frac{1 \space yd }{3 \space ft}=1,256 \space yd\)
6- A
3,400 out of 74,800 equals to \(\frac{3,400}{74,800}=\frac{17}{374}=\frac{1}{22}\)
7- A
Prime factorizing of \(20=2×2×5\)
Prime factorizing of \(12=2×2×3\)
LCM\(=2×2×3×5=60\)
8- C
Plug in the value of \(x\) into the function f. First, plug in 3.1 for \(x\).
\(A. f=2x-\frac{3}{10}=2(3.1)-\frac{3}{10}=5.9≠8.6\)
\(B. f=x+\frac{3}{10}=3.1+\frac{3}{10}=3.4≠10.8\)
\(C. f=2x+2 \frac{2}{5}=2(3.1)+2 \frac{2}{5}=6.2+2.4=8.6 \)
This is correct!
Plug in other values of \(x. x=4.2\)
\(f=2x+2\frac{2}{5} =2(4.2)+2.4=10.8 \)
This one is also correct.
\(x=5.9\)
\(f=2x+2 \frac{2}{5}=2(5.9)+2.4=14.2 \)
This one works too!
\(D. 2x+\frac{3}{10}=2(3.1)+\frac{3}{10}=6.5≠8.6\)
9- D
1 kg\(=\) 1000 g and 1 g \(=\) 1000 mg
96 kg\(=\) 96 \(×\) 1000 g \(=\)96 \(×\) 1000 \(×\) 1000 \(=\)96,000,000 mg
10- B
The diameter of a circle is twice the radius. Radius of the circle is \(\frac{25}{2}\).
Area of a circle = \(πr^2=π(\frac{25}{2})^2=156.25π=156.25×3.14=490.625≅491\)
Looking for the best resource to help you succeed on the MAP Math Grade 6 Math test?
The Best Books to Ace 6th Grade MAP Math Test
Common Core Math Exercise Book for Grade 6 Student Workbook and Two Realistic Common Core Math Tests
Related to This Article
More math articles
- High School Placement Test (HSPT): Complete Guide
- Word Problems Involving Writing a Ratio
- Overview of the GED Mathematical Reasoning Test
- Best Calculator for Calculus 2023
- 5th Grade DCAS Math Worksheets: FREE & Printable
- 5th Grade ACT Aspire Math Worksheets: FREE & Printable
- The Ultimate 7th Grade K-PREP Math Course (+FREE Worksheets)
- 10 Most Common 4th Grade Georgia Milestones Assessment System Math Questions
- Top Free Websites for FTCE General Knowledge Math Preparation
- How to Perform Scalar Multiplication
What people say about "6th Grade MAP Math Practice Test Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.