How to Graph Logarithmic Functions?

Logarithmic functions are closely related to exponential functions and are considered as an inverse of the exponential function. The exponential function \(a^x = N\) is transformed to a logarithmic function \(log _a\left(N\right)=x\).

Related Topics

• How to Solve Natural Logarithms
• How to Use Properties of Logarithms
• How to Evaluate Logarithm

A step-by-step guide to graphing logarithmic functions

Domain and range of logarithmic functions

We know that \(log x\) is defined only when \(x > 0\). So the domain is the set of all positive real numbers. We can see that \(y\) can be either a positive or negative real number (or) it can be zero as well. Thus, \(y\) can take the value of any real number.

Note:

• The domain of \(log\) function \(y = log x\) is \(x > 0\) (or) \((0, ∞)\).
• The range of any log function is the set of all real numbers \((R)\).

Logarithmic graph

We know that exponential and \(log\) functions are inversely proportional to each other, and so their graphs are symmetric concerning the line \(y = x\). Also, note that \(y = 0\) when \(x = 0\) as \(y=log _a\left(1\right)=0\) for any \(a\). Thus, all such functions have an \(x\)-intercept of \((1, 0)\).  A logarithmic function doesn’t have a \(y\)-intercept as \(log _a\:0\) is not defined.

Properties of logarithmic graph

• \(a>0\) and \(a≠1\).
• The logarithmic graph increases when \(a>1\) and decreases when \(0<a<1\).
• The domain is obtained by setting the argument of the function greater than \(0\).
• The range is the set of all real numbers.

Graphing logarithmic functions

Before plotting the log function, just have an idea of whether you get an increasing curve or decreasing curve as the answer. If the \(base > 1\) then the curve is increasing, and if \(0 < base < 1\), then the curve is decreasing. 

Here are the steps for graphing logarithmic functions:

• Find the domain and range.
• Find the vertical asymptote by setting the argument equal to \(0\). Note that a \(log\) function doesn’t have any horizontal asymptote.
• Substitute some value of \(x\) that makes the argument equal to \(1\) and use the property \(log _a\left(1\right)=0\). This gives us the \(x\)-intercept.
• Substitute some value of \(x\) that makes the argument equal to the base and use the property \(log _a\left(a\right)=1\) This would give us a point on the graph.
• Connect the two points (from the last two steps) and extend the curve on both sides relative to the vertical asymptote.

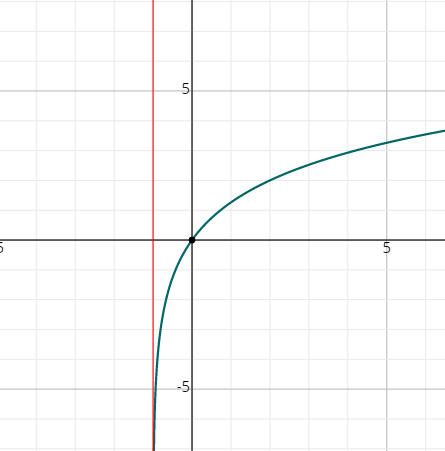
Graphing Logarithmic Functions – Example 1:

Graph the logarithmic function \(f\left(x\right)=2\:log _3\left(x+1\right)\).

Solution:

The base is \(3 > 1\). So the curve would be increasing.

The domain of the function is: \(x + 1 > 0 ⇒ x > -1\), so domain \(= (-1, ∞)\).

The range is \(= R\).

Vertical asymptote is \(x = -1\).

At \(x = 0\), \(y=2\:log _3\left(x+1\right)=2\:log _3\left(0+1\right)=2\:log _31=2(0)=0\)

At \(x = 2\), \(y=2\:log _3\left(x+1\right)=2\:log _3\left(2+1\right) =2\:log _33=2(1)=2\)

(If we want more clarity, we can make a table of values with random values of \(x\) and replace each one in the given function to calculate the values of \(y\). This way we get more points in the chart and it helps to complete the chart.)

Thus, \((0, 0)\) and \((2, 2)\) are two points on the curve. Thus, the \(log\) function graph looks as follows.

Exercises for Graphing Logarithmic Functions

Plot the following Logarithmic functions.

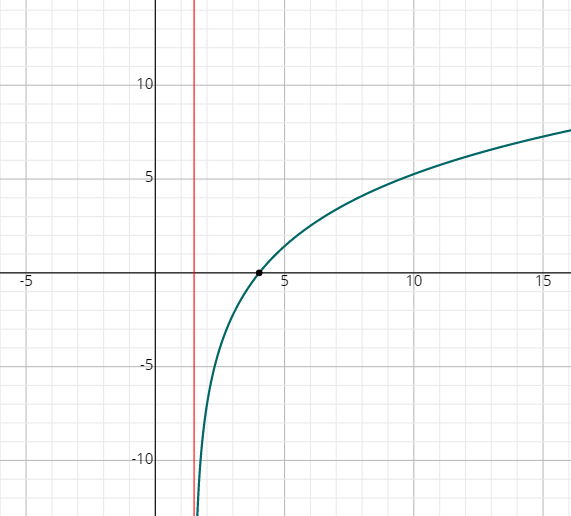
• \(\color{blue}{f\left(x\right)\:=\:3\:log _2\left(2x-3\right)-7}\)

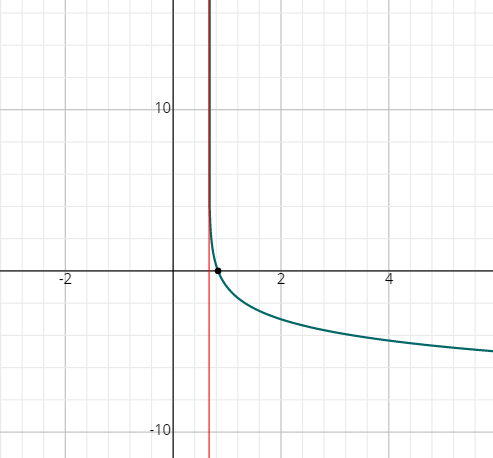
• \(\color{blue}{f\left(x\right)\:=\:-2\:log _4\left(6x-4\right)}\)

\(\color{blue}{f\left(x\right)\:=\:3\:log _2\left(2x-3\right)-7}\)

• \(\color{blue}{f\left(x\right)\:=\:-2\:log _4\left(6x-4\right)}\)

Recommended EffortlessMath Books

For a workbook that builds logarithmic graphs into a full exponential-and-log unit, the Algebra II for Beginners walks through every transformation with worked examples. For pre-calc-level coverage that prepares you for calculus and natural logs, see the Pre-Calculus for Beginners.

Algebra II for Beginners 2026 The Ultimate Step by Step Guide to Acing Algebra II

Download

$27.99 Original price was: $27.99.$17.99Current price is: $17.99.

Rated 5.00 out of 5 based on 1 customer rating

Satisfied 1 Students

Frequently Asked Questions

How do you graph a logarithmic function?

Identify the base and any transformations, draw the vertical asymptote, plot a few key points (\((1,0)\) and \((b,1)\) for the parent function), and sketch a smooth curve that approaches the asymptote on one side and rises slowly on the other. Whether the curve rises or falls depends on whether the base is greater than or less than 1.

What is the parent log function?

\(y=\log_b(x)\) for some base \(b>0\), \(b\neq 1\). The most common parents are \(y=\log(x)\) (base 10) and \(y=\ln(x)\) (base \(e\approx 2.718\)). All log parent functions pass through \((1,0)\) and have a vertical asymptote at \(x=0\).

What is the domain of a logarithmic function?

The argument of a log must be strictly positive, so for \(y=\log_b(x)\), the domain is \(x>0\). For \(y=\log_b(x-h)\), the domain is \(x>h\) — solve the inside of the log greater than zero. The range is always all real numbers.

What is the vertical asymptote of a log function?

For \(y=\log_b(x)\), the vertical asymptote is \(x=0\). For \(y=\log_b(x-h)\), it moves to \(x=h\). The graph approaches but never touches the asymptote, because the argument of the log can get arbitrarily close to zero but never reach it.

How are log and exponential graphs related?

They are reflections of each other across the line \(y=x\), because logs and exponentials are inverse functions. If \((a,b)\) is on \(y=2^x\), then \((b,a)\) is on \(y=\log_2(x)\). The exponential has a horizontal asymptote at \(y=0\); the log has a vertical asymptote at \(x=0\).

How do you graph natural log?

Same way as any log, with base \(e\approx 2.718\). \(y=\ln(x)\) passes through \((1,0)\), passes through \((e,1)\approx (2.72, 1)\), and has a vertical asymptote at \(x=0\). For a quick shape, plot \((1,0)\), \((e,1)\), and \((e^2, 2)\approx (7.39, 2)\).

What happens when the base is less than 1?

When \(0

How do you find x and y intercepts of a log function?

For \(y=\log_b(x-h)+k\): the y-intercept exists only when \(x=0\) is in the domain (i.e., \(h<0\)). The x-intercept is where \(y=0\), giving \(\log_b(x-h)=-k\), so \(x-h=b^{-k}\), so \(x=h+b^{-k}\). Many log functions have no y-intercept because their asymptote is at or to the right of \(x=0\).

How do transformations shift a log graph?

\(y=a\log_b(x-h)+k\): the \(h\) shifts horizontally (right if \(h>0\), left if \(h<0\)), \(k\) shifts vertically, \(a\) stretches vertically (and flips if \(a<0\)). The asymptote moves to \(x=h\). The key point \((1,0)\) moves to \((h+1, k)\).

Why does the log curve grow so slowly?

Because logs are inverses of exponentials, and exponentials grow fast. To make \(\log_{10}(x)\) reach 1, \(x\) has to reach 10; to reach 2, \(x\) must reach 100; to reach 3, \(x\) must reach 1,000. So the y-value barely climbs while \(x\) sprints. This is why log scales are used to plot data that span many orders of magnitude.

Related EffortlessMath Lessons

If a topic on this page feels rusty, these short lessons go deeper:

• How to solve natural logarithms
• Properties of logarithms
• How to graph exponential functions
• How to verify inverse functions
• Rules of exponents