How to Graph the Cosecant Function?
The cosecant function is the reciprocal of the trigonometric function sine. In this guide, you will learn more about the graph of the cosecant function.
Graph the Cosecant Function: what to notice and how to work it
What to notice first
Common student mistake
Key formulas and cues
A reliable path
- Choose the modelUse a right triangle, the unit circle, or a transformed graph.
- Track unitsConvert degrees and radians when needed.
- Use identitiesReplace complicated trig expressions with equivalent simpler ones.
Worked examples
Find secant asymptotes
- Secant is 1/cosine.
- Asymptotes occur where cosine is 0.
- Cosine is 0 at pi/2 plus multiples of pi.
Find cosecant asymptotes
- Cosecant is 1/sine.
- Asymptotes occur where sine is 0.
- Sine is 0 at multiples of pi.
Try one before moving on
Graph the Cosecant Function: pop-up practice
A step-by-step guide to graphing the cosecant function
The cosecant function is the reciprocal of the trigonometric function \(sin\). Since the cosecant function is the reciprocal of the \(sin\) function, we can write its formula as:
\(\color{blue}{csc (\theta)=\frac{Hypotenuse}{opposite\: side}=\frac{1}{sin\:\theta}}\)
\(cosec x\) is defined for all real numbers except for values where \(sin x\) is equal to zero. Therefore, we have vertical asymptotes at points where \(csc x\) is not defined. Also, using the values of \(sin x\), we have \(y=csc x\) as:
- When \(x = 0\), \(sin x = 0\) \(\rightarrow\) \(csc x =\) not defined
- When \(x = \frac{\pi }{6}\), \(sin x = \frac{1}{2}\)\(\rightarrow\) \(csc x = 2\)
- When \(x =\frac{\pi }{4}\), \(sin x=\frac{1}{\sqrt{2}}\)\(\rightarrow\) \(csc x = \sqrt{2}\)
- When \(x =\frac{\pi }{3}\), \(sin x= \frac{\sqrt{3}}{2}\)\(\rightarrow\) \(csc x = \frac{2}{\sqrt{3}}\)
- When \(x =\frac{\pi }{2}\), \(sin x = 1\)\(\rightarrow\) \(csc x=1\)
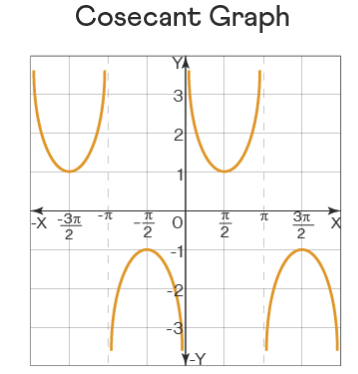
Therefore, by drawing the above points on a graph and connecting them, we have the cosecant graph as follows:
Related to This Article
More math articles
- Complete Guide to Mastering Logic and Truth Tables
- 8th Grade OST Math Worksheets: FREE & Printable
- The Ultimate 7th Grade MAP Math Course (+FREE Worksheets)
- What Are the 4 Methods to Prove Triangles Are Congruent?
- Accuplacer Math Formulas
- How to Create a Proportion? (+FREE Worksheet!)
- Free Grade 6 English Worksheets for Maryland Students
- Magnetism
- How to Use Models to Divide Whole Numbers by Unit Fractions?
- 10 Most Common Pre-Algebra Math Questions
What people say about "How to Graph the Cosecant Function? - Effortless Math"?
No one replied yet.