Full-Length 7th Grade PSSA Math Practice Test-Answers and Explanations
Did you take the 7th Grade PSSA Math Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.
7th Grade PSSA Math Practice Test Answers and Explanations
1- Choice C is correct.
If the score of Mia was 90, then the score of Ava is 30. Since the score of Emma was one and a half as that of Ava, therefore, the score of Emma is 1.5 × 30 = 45.
2- Choice A is correct
Write the ratio and solve for \(x\).
\( \frac{60}{50}=\frac{5x+2}{10}⇒ 12=5x+2 ⇒12-2=5x⇒ x=\frac{10}{5}=2\)
3- Choice B is correct
Let \(x\) be the number of students in the class. \(40\%\) of \(x\) = girls, \(25\%\) of girls = tennis player,
Find \(25\%\) of \(40\%\). Then: \(25\%\) of \(40\%=0.25×0.40=0.1=10\%\) or \(\frac{10}{100}=\frac{1}{10}\)
4- Choice C is correct
Use the information provided in the question to draw the shape.
Use Pythagorean Theorem: \(a^2+b^2=c^2\)
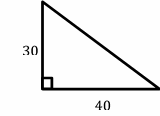
\(30^2+40^2=c^2⇒ 900+1600= c^2⇒2500= c^2⇒c=50\)
5- Choice A is correct
Write a proportion and solve for \(x\).
\( \frac{12 \space Cans}{$ 7.40}=\frac{30 \space Cans}{x }, x= \frac{7.40×30}{12} ⇒x=$18.5\)
The Absolute Best Book to Ace the 7th Grade PSSA Math Test
6- Choice D is correct
Use the volume of square pyramid formula.
\(V= \frac{1}{3} a^2 h ⇒V=\frac{1}{3} (12 \space m)^2×20 \space m ⇒ V=960 \space m^3\)
7- Choice C is correct
Let \(x\) be the number of soft drinks for 240 guests. Write a proportional ratio to find \(x\). \(\frac{6 \space soft \space drinks}{8 \space guests}=\frac{x}{240 \space guests}, x=\frac{240×6}{8}⇒x=180\)
8- Choice B is correct
Use the formula for Percent of Change: \(\frac{New \space Value-Old \space Value}{Old \space Value}×100\%, \frac{1.75-1.4}{1.4}×100\%=25\%\)
9- The answer is: \(-99\)
Use PEMDAS (order of operation):
\([8×(-14)+15]-(10)+[4×6]÷3=[-122+15]-(10)+8=-97-10+8=-99\)
10- Choice D is correct
Simplify. \(5x^2 y(2xy^3)^4=5x^2 y(16x^4 y^{12} )=80x^6 y^{13}\)
Best 7th Grade PSSA Math Prep Resource for 2022
11- Choice C is correct
The distance between Jason and Joe is 14 miles. Jason running at 6 miles per hour and Joe is running at the speed of 8 miles per hour. Therefore, every hour the distance is 2 miles less.
14 ÷ 2 = 7
12- Choice A is correct.
Let x be the integer. Then: \(5x-9=101\), Add 9 both sides: \(5x=110\), Divide both sides by 5: \(x=22\)
13- Choice D is correct
Two and half times of 18,000 is 45,000. One-fifth of them canceled their tickets.
One sixth of \(45,000\) equals \(9,000(\frac{1}{5} × 45000=9000)\).
\(36,000(45000-9000=36000)\) fans are attending this week
14- Choice C is correct
Write the numbers in order: \(25,12,13,18,22,36,22\)
Since we have 7 numbers (7 is odd), then the median is the number in the middle, which is 22.
15- Choice D is correct.
The question is: 615 is what percent of 820?
Use percent formula: \(part=\frac{percent}{100}×whole\)
\(615=\frac{percent}{100}×820 ⇒ 615=\frac{percent ×820}{100}⇒61,500=percent×820\) ⇒
\(percent=\frac{61,500}{820}=75\), \(615\) is \(75\%\) of \(820\). Therefore, the discount is: \(100\%-75\%=25\%\)
16- The answer is \(22 \frac{1}{3}\) miles.
Robert runs \(4 \frac{1}{3}\) miles on Saturday and \(2(4 \frac{1}{3})\) miles on Monday and Wednesday.
Robert wants to run a total of 35 miles this week. Therefore, subtract 4 \(\frac{1}{3}+2(4 \frac{1}{3})\) from 35.
\(35-(4 \frac{1}{3}+2(4 \frac{1}{3} ))=35-12 \frac{2}{3}=22 \frac{1}{3}\) miles
17- Choice B is correct
To find the area of the shaded region, find the difference of the area of two circles. \(S_1\): the area of bigger circle. \(S_2\): the area of the smaller circle). Use the area of circle formula. \(S=πr^2\)
\(S_1- S_2=π(6 \space cm)^2- π(4 \space cm)^2⇒S_1- S_2=36π \space cm^2-16π \space cm^2 ⇒ S_1- S_2 =20π \space cm^2\)
18- Choice A is correct
Use Pythagorean Theorem: \(a^2+b^2=c^2\),
\(12^2+5^2=c^2⇒ 144+25= c^2 ⇒ c^2=169 ⇒c=13\)
19- Choice A is correct
Let L be the price of the laptop and C be the price of the computer. 4(L) =7(C) and L = $240 + C
Therefore, 4($240 + C) =7C ⇒ $960 + 4C = 7C ⇒ C=$320
20- The answer is 70.
Jason needs an \(75\%\) average to pass five exams. Therefore, the sum of 5 exams must be at least \(5×75=375\), The sum of 4 exams is \(62+73+82+88=305\).
The minimum score Jason can earn on his fifth and final test to pass is:
\( 375-305=70\)
The Best Books to Ace the 7th Grade PSSA Math Test
Related to This Article
More math articles
- How to Interpret Categorical Data
- How to Compare Amounts of Money?
- Top 10 Tips You MUST Know to Retake the CBEST Math
- CBEST Test Facts and FAQs
- HiSET Math – Test Day Tips
- How to Remove Ambiguity in Infinite Limits
- 10 Most Common 4th Grade PSSA Math Questions
- Using Number Lines to Add Two Integers with Different Signs
- Number Properties Puzzle – Challenge 5
- How to Transform Linear Functions
What people say about "Full-Length 7th Grade PSSA Math Practice Test-Answers and Explanations - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.