Full-Length CLEP College Mathematics Practice Test-Answers and Explanations
Did you take the CLEP College Mathematics Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.
CLEP College Mathematics Reasoning Practice Test Answers and Explanations
1- Choice C is correct
In order to figure out what the equation of the graph is, first find the vertex. From the graph, we can determine that the vertex is at \((1,2)\). We can use vertex form to solve the equation of this graph. Recall vertex form, \(y=a(x-h)^2+k\), where \(h\) is the x coordinate of the vertex, and k is the y coordinate of the vertex. Plugging in our values, you get \(y=a(x-1)^2+2\)
To solve for a, we need to pick a point on the graph and plug it into the equation.
Let’s pick \((-1,10)\).
\(10=a(-1-1)^2+2→10=a(-2)^2+2→10=4a+2\)
\(8=4a→a=2\) Now the equation is : \(y=2(x-1)^2+2\)
Let’s expand this, \(y=2(x^2-2x+1)+2→y=2x^2-4x+2+2→y=2x^2-4x+4\)
The equation in Choice C is the same.
2- Choice D is correct
Use Pythagorean Theorem: \(a^2+b^2=c^2\). \(→82 + 152 = c2 ⇒ 64+225=c2 ⇒ 289=c^2⇒c=17\)
3- Choice D is correct
A={1,5,10,15,20}, B={3,6,9,12}, C={2,4,6,8,10,12,14}
The union of A and B is: A∪B={1,3,5,6,9,10,12,15,20}
The intersection of (A∪B) and C is: (A∪B)∩C={6,10,12}
4- Choice D is correct
Subtracting 7 to each side of the inequality yields the inequality. Therefore, the least possible value is.
5- Choice D is correct
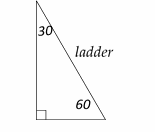
The relationship among all sides of a special right triangle
\(30°-60°- 90°\) is provided in this triangle:
In this triangle, the opposite side of the \(30°\) angle is half of the hypotenuse.
Draw the shape of this question:
The ladder is the hypotenuse. Therefore, the ladder is \(70\) ft.
6- Choice B is correct
A={1,4,7,10,13,16,19}, B={1,4,8,12,16,20}
The intersection of A and B is: A∩B={1,4,16}. There are 3 elements in A∩B.
The Absolute Best Book to Ace the CLEP College Mathematics Test
7- Choice B is correct
\(|x+8|≤5→-5≤x+8≤5→-5-8≤x+8-8≤5-8→-13≤x≤-3\)
8- Choice C is correct
Use simple interest formula: I=prt (I = interest,p = principal,r = rate,t = time)
I=(12,000)(0.055)(8)=5,280
9- Choice A is correct
The area of the circle is less than 81 π. Use the formula of areas of circles.
\(Area=πr^2 ⇒ 81 π> πr^2⇒ 81>r^2⇒ r<9\)
The radius of the circle is less than \(9\). Let’s put 9 for the radius. Now, use the circumference formula: \(Circumference =2πr=2π (9)=18π\), Since the radius of the circle, is less than \(9\). Then, the circumference of the circle must be less than \(18 π\). Only choice A is less than \(18 π\).
10- Choice D is correct
\(\begin{cases}2x+4y=-10 \\6x+3y=6 \end{cases}\)→Multiply the top equation by -3 then,
\(\begin{cases}-6x-12y=30\\6x+3y=6 \end{cases}\)→ Add two equations. -9y=36→y=-4 , plug in the value of y into the first equation: \(2x+4y=-10→2x+4(-4)=-10\)
Added 16 to both sides of the equation. \(2x-16=-10 →2x-16+16=-10+16=6 →2x=6 →x=3\)
11- Choice D is correct
Write the equation and solve for B: 0.80 A = 0.16 B, divide both sides by 0.16, then:
0.80/0.16 A=B, therefore: B=5A, and B is 5 times of A or it’s 500% of A.
12- Choice B is correct
Use this formula: Percent of Change=\(\frac{New \space Value-Old \space Value}{Old \space Value}×100%\) \(\rightarrow\) \(\frac{24000-30000}{30000}×100%\)
\(= 20\%\) and \(\frac{19200-24000}{24000}×100\%=20\%\)
13- Choice C is correct
If the length of the box is 48, then the width of the box is one fourth of it, 12, and the height of the box is 6 (one second of the width). The volume of the box is: \(V=lwh=(48)(12)(6)=3,456\)
14- Choice D is correct
To find the number of possible outfit combinations, multiply number of options for each factor: \(5×4×3=60\)
15- Choice B is correct
The percent of girls playing tennis is: \(60 % × 22 % = 0.60 × 0.22 = 0.132 = 13.2 %\)
16- Choice B is correct
Use this formula: Percent of Change=\(\frac{New \space Value-Old \space Value}{Old \space Value}×100%\) \(\rightarrow\) \(\frac{48-64}{64}×100\%=-25\%\)
(Negative sign here means that the new price is less than old price).
17- Choice C is correct
Use percent formula: \(part = \frac{percent}{100} ×whole\)
\(48 = \frac{percent}{100} ×24 ⇒ 48=\frac{percent ×24}{100}\), multiply both sides by 100.
4800=percent ×24, divide both sides by 24.
200=percent
18- Choice B is correct
The area of the trapezoid is: Area=\(\frac{1}{2} h(b_1+b_2\)=\(\frac{1}{2})(x)(18+12)\)=120→15x=120→x=8. y=\(\sqrt{6^2+8^2}\)=\(\sqrt{36+}{64}\)=\(\sqrt{100}\)=10
The perimeter of the trapezoid is: 8+12+10+18=48
19-Choice C is correct
Add the first 4 numbers.55+68+48+72=243
To find the distance traveled in the next 4 hours, multiply the average by number of hours. Distance = Average × Rate =64×4=256. Add both numbers. 243+256=499
20-Choice C is correct
Use distance formula: Distance = Rate × time ⇒ 468=72×T, divide both sides by 72. \(\frac{468}{72}\)=T →T=6.5 hours. Change hours to minutes for the decimal part. 0.5 hours = 0.5×60=30 minutes.
21-Choice D is correct
The equation of a line is in the form of \(y=mx+b\), where m is the slope of the line and b is the y-intercept of the line. Two points (5, -2) and (3, 4) are on line A. Therefore, the slope of the line A is: slope of line A=\(\frac{y_2- y_1}{x_2 – x_1}\)= \(\frac{4-(-2)}{(3-5}\)=\(\frac{6}{-2}=-3\)
The slope of line A is -3. Thus, the formula of the line A is:\(y=mx+b=-3x+b\), choose a point and plug in the values of x and y in the equation to solve for b. Let’s choose point (5, -2). Then:\( y=-3x+b→-2=-3(5)+b→b=-2+15=13\)
The equation of line A is:\(y=-3x+13\). Now, let’s review the choices provided:
A. (-1,1) \(y=-3x+13→1=-3(-1)+13=16\) This is not true.
B. (2,3) \(y=-3x+13→3=-3(2)+13=7\) This is not true.
C. (3,2) \(y=-3x+13→2=-3(3)+13=4\) This is not true.
D. (4,1) \(y=-3x+13→1=-3(4)+13=1\) This is true!
22-Choice B is correct
Let \(x\) be the number. Write the equation and solve for \(x\).
\(\frac{1}{3}×(27)\)=\(\frac{3}{4}\) . \(x\) ⇒ \(\frac{1×27}{3}=\frac {3x}{4}\) , use cross multiplication to solve for \(x\). \(4×27=3x×3 ⇒108=9x ⇒ x=12\)
23-Choice D is correct
To find the discount, multiply the number by \((100\%\) – rate of discount). Therefore, for the first discount we get: (D) \((100\% – 15\%)\) = \((D) (0.85)\) = 0.85 D For increase of \(20\%\): \((0.85 D)\) \((100\% + 20\%)\) =\( (0.85 D) (1.20)\) = 1.02 D = \(102\%\) of D
24-Choice C is correct
First, find the equation of the line. All lines through the origin are of the form \(y=mx\), so the equation is \(y=\frac{1}{4} x\). Of the given choices, only choice C \((4, 1)\), satisfies this equation: \(y=\frac{1}{4}x→1=\frac{1}{4} (4)=1\)
25-Choice C is correct
The area of the floor is: 8 cm × 22 cm = 176 cm2
The number of tiles needed = 176 ÷ 11 = 16
26-Choice D is correct
Let’s compare each fraction: \(\frac{5}{13}<\frac{4}{7}<\frac{3}{5}<\frac{7}{9}\) Only choice D provides the right order.
27- Choice C is correct
Use the information provided in the question to draw the shape.
Use Pythagorean Theorem: \(a^2+ b^2=c^2\)
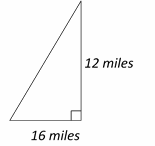
\(12^2+ 16^2=c^2 ⇒ 144+256= c^2 ⇒ 400=c^2 ⇒ c=20\)
28- Choice A is correct
The ratio of boy to girls is 5 : 7. Therefore, there are 5 boys out of 12 students. To find the answer, first, divide the total number of students by 12, then multiply the result by 5.
\(60÷12=5 ⇒ 5×5=25\). There are 25 boys and \(35 (60-25)\) girls. So, 10 more boys should be enrolled to make the ratio 1:1
29- Choice A is correct
The question is this: 535.44 is what percent of 582? Use percent formula: \(part=\frac{percent}{100}×whole. 535.44=\frac{percent}{100}×582 ⇒ 535.44= \frac{percent ×582}{100} ⇒ 53544 =percent ×582 ⇒ percent=\frac{53544}{582}=92\)
53544 is \(92\%\) of 582. Therefore, the discount is: \(100\% –92\%=8\%\)
30- Choice D is correct
If the score of Mia was 30, therefore the score of Ava is 60. Since the score of Emma was half as that of Ava, therefore, the score of Emma is 120.
31- Choice D is correct
If 18 balls are removed from the bag at random, there will be one ball in the bag.
The probability of choosing a brown ball is 1 out of 19. Therefore, the probability of not choosing a red ball is 18 out of 19 and the probability of having not a red ball after removing 18 balls is the same.
32- Choice D is correct
Let \(x\) be the smallest number. Then, these are the numbers:
\(x, x+1, x+2, x+3, x+4\)
\(average =\frac{sum of terms }{number of terms} ⇒ 45=\frac{x+(x+1)+(x+2)+(x+3)+(x+4)}{5}⇒45=\frac{5x+10}{5} ⇒ 225=5x+10 ⇒ 215=5x ⇒ x=43\)
33- Choices D is correct
Some of prime numbers are: 2, 3, 5, 7, 11, 13. Find the product of two consecutive prime numbers: 2 × 3 = 6 (not in the options), 3 × 5 = 15 (bingo!), 5 × 7 = 35 (not in the options)
7 × 11 = 77 (not in the options)
34- Choice C is correct
The slop of line A is: m\(=\frac{y_2-y_1)}{x_2-x_1}=\frac{8-2}{6-4}=\frac{6}{2}=3\)
Parallel lines have the same slope and only choice C \((y=3x-1)\) has slope of 1.
35- Choice B is correct
\(15\%\) of the volume of the solution is alcohol. Let \(x\) be the volume of the solution.
Then: \(15\%\) of \(x=36\) ml ⇒ \(0.15 x=36 ⇒ x=36÷0.15=240\)
36- Choice B is correct
average \(=\frac{sum \space of \space terms}{number \space of \space terms}\)
The sum of the weight of all girls is: \(24×68=1632\) kg
The sum of the weight of all boys is: \(16×75=1200\) kg
The sum of the weight of all students is: \(1632+1200=2832\) kg
average\(=\frac{2832}{40}=70.8\)
37- Choice A is correct
Subtracting \(2x\) and adding 6 to both sides of \(3x-6≥2x-8\) gives \(x ≥-2\). Therefore, \(x\) is a solution to \(3x-6≥2x-8\) if and only if \(x\) is greater than or equal to \(-2\) and \(x\) is NOT a solution to \(3x-6≥2x-8\) if and only if \(x\) is less than \(-2\). Of the choices given, only \(-3\) is less than \(-2\) and, therefore, cannot be a value of \(x\).
38- Choice D is correct
Given the two equations, substitute the numerical value of a into the second equation to solve for \(x\). \(a=\sqrt{5}, 6a=\sqrt{3x}\), Substituting the numerical value for a into the equation with is as follows. \(6(\sqrt{5})=\sqrt{3x}\),Now square both side of the equation. \((6\sqrt{5})^2=(\sqrt{3}x)^2\)
Remember to square both terms within the parentheses. Also, recall that squaring a square root sign cancels them out. \(6^2 \sqrt{5}^2=3x, 36(5)=3x, 180=3x, x=60\)
Best CLEP College Mathematics Prep Resource for 2022
39- Choice A is correct
Formula for the Surface area of a cylinder is: \(SA=2πr^2+2πrh→130π=2πr^2+2πr(8)→r^2+8r-65=0→(r+13)(r-5)=0→r=5\) or \(r=-13\) (unacceptable)
40- Choice A is correct
Let \(x\) be the number of years. Therefore, $1,200 per year equals \(1,200x\).
starting from $14,400 annual salary means you should add that amount to \(1,200x\).
Income more than that is: \(I > 1200x + 14400\)
41- Choice B is correct
A zero of a function corresponds to an \(x\)-intercept of the graph of the function in the \(xy\)-plane. Therefore, the graph of the function \(g(x)\), which has four distinct zeros, must have four \(x\)-intercepts. Only the graph in choice C has four \(x\)-intercepts.
42- Choice D is correct
\(0.3x=(0.45)×24→x=36→(x-6)^2=(36-6)^2=30^2=900\)
43- Choice C is correct
The weight of 14.6 meters of this rope is: 14.6 × 600 g = 8,760) g
1 kg = 1,000 g, therefore, 8,760 g ÷ 1000 = 8.76 kg
44- Choice B is correct
\(y=5a^2 b-3ab^3\). Plug in the values of \(a\) and \(b\) in the equation: \(a = 2\) and \(b = -1\)
\(y=5(2)^2 (-1)-3(2) (-1)^3=-5(4)+6=-20+6=-14\)
45- Choice C is correct
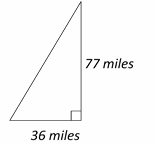
Use the information provided in the question to draw the shape.
Use Pythagorean Theorem: \(a^2 + b^2 = c^2\)
\(362 + 772 = c^2 ⇒ 1,296 + 5,929 = c^2 ⇒ 7,225 = c^2 ⇒ c = 85\)
46- Choice C is correct
The four-term polynomial expression can be factored completely, by grouping, as follows: \((x^3-7x^2 )+(4x-28)=0\)
\(x^2 (x-7)+4(x-7)=0 (x-7)(x^2+4)=0\)
By the zero-product property, set each factor of the polynomial equal to 0 and solve each resulting equation for \(x\). This gives \(x=7\) or \(x=±i\sqrt{4} =±i2\), respectively. Because the equation the question asks for the real value of \(x\) that satisfies the equation, the correct answer is 7.
47- Choice C is correct.
To solve for \(f(7g(P))\), first, find \(7g(p)\). \(g(x)=\log_{7}{x} →g(p)=\log_{7}{p}→7g(p)=7\log_{7}{p}=\log_{7}{p^7}\)⇒ Now, find \(f(7g(p))\): \(f(x)=7^x→f(\log_{7}{p^7})=7^{\log_{7}{p^7}}\)
Logarithms and exponential with the same base cancel each other. This is true because logarithms and exponential are inverse operations. Then: \(f(\log_{7}{p^7} )=7^{\log_{7}{p^7}}=p^7\)
48- Choice C is correct
$0.98 per minute to use car. This per-minute rate can be converted to the hourly rate using the conversion 1 hour = 60 minutes, as shown below.
\(\frac{0.98}{minute}×\frac{60 \space minutes}{1 \space hours}=\frac{0.98×60}{hour}\)
Thus, the car costs $(0.98×60) per hour. Therefore, the cost c, in dollars, for \(h\) hours of use is c = (0.98×60)h, Which is equivalent to c = 0.98(60h)
49- Choice D is correct
The best way to deal with changing averages is to use the sum. Use the old average to figure out the total of the first 3 scores: Sum of first 3 scores:
(3)(90) = 270
Use the new average to figure out the total she needs after the 4th score: Sum of 4 score: (4)(92) = 368, To get her sum from 270 to 368, Mary needs to score 368 – 270 = 98.
50- Choice C is correct
To solve a quadratic equation, put it in the \(ax^2+bx+c=0\) form, factor the left side, and set each factor equal to 0 separately to get the two solutions. To solve \(x^2=24-5x\) , first, rewrite it as \(x^2+5x-24=0\). Then factor the left side: \(x^2+5x-24=0 , (x-3)(x+8)=0\)
\(x=3\) or \(x=-8\), There are two solutions for the equation.
51- Choice A is correct
Replace \(z\) by \(\frac{z}{3}\) and simplify.
\(\frac{8y+\frac{r}{r+1}}{\frac{\frac{6}{z}}{2}}=\frac{8y+\frac{r}{r+1}}{\frac{2×6}{z}}=\frac{8y+\frac{r}{r+1}}{2×\frac{6}{z}}=\frac{1}{2}×\frac{8y+\frac{r}{r+1}}{\frac{6}{z}}=\frac{x}{2}\)
52- Choice B is correct
\(f(x)=x^3-4x^2+3x-6,g(x)=3\), then \(f(g(x))=f(3)=(3)^3-4(3)^2+3(3)-6=-6\)
53- Choice A is correct.
Let the number be \(A\). Then: \(a=b\% ×A\). Solve for \(A\). \(a=\frac{b}{100}×A\)
Multiply both sides by \(\frac{100}{b}: a×\frac{100}{b}=\frac{b}{100}×\frac{100}{b}×A→A=\frac{100a}{b}\)
54- Choice D is correct
The line passes through the origin, (7, m) and (m , 14).
Any two of these points can be used to find the slope of the line. Since the line passes through (0 , 0) and (7 , m), the slope of the line is equal to \(\frac{m-0}{7-0}=\frac{m}{7}\). Similarly, since the line passes through (0 , 0) and (m , 14), the slope of the line is equal to \(\frac{14-0}{m-0}=\frac{14}{m}\). Since each expression gives the slope of the same line, it must be true that \(\frac{m}{7}=\frac{14}{m}\)
Using cross multiplication gives
\(\frac{m}{7}=\frac{14}{m}→m^2=7×14=98 →m=±\sqrt{98}=±\sqrt{49×2}=±\sqrt{49}×\sqrt{2}=±7\sqrt{2}\)
55- Choice B is correct
It is given that \(g(8)=6\). Therefore, to find the value of \(f(g(8))\), then \(f(g(8))=f(6)=4\)
56- Choice C is correct
Plug in each pair of number in the equation:
A. \((-1, 2): 3(-1)-2(2)=-7\) Nope!
B. \((1, 3): 3(1)-2(3)=-3\) Nope!
C. \((2, -3): 3(2)-2(-3)=12\) Bingo!
D. \((2, 2): 3(2)-2(2)=2\) Nope!
57- Choice B is correct
Here we can substitute 7 for \(x\) in the equation. Thus, \(3y+3=6(7-4), → 3y+3=18\)
Subtracting 3 to both side of the equation: \(3y=18-3=15,→ 3y=15\) → divide two sides by 3, \(y=5\)
58- Choice A is correct
Let’s review the options: I. \(|a|<1→-1<a<1\)
Multiply all sides by \(b\). Since, \(b>0→-b<ba<b\)
II. Since, \(-1<a<1\), and \(a<0→-a>a^2>a\) (plug in \(-\frac{1}{2}\), and check!)
III. \(-1<a<1\), multiply all sides by 4, then:
\(-4<4a<4\), sutract 3 from all sides,then:
\(-4-3<4a-3<4-3→-7<4a-3<1\)
I only incorrect.
59- Choice C is correct
The equation can be rewritten as
\(c-d=ac\)→(divide both sides by \(c\)) \(1-\frac{d}{c}=a\), since c < 0 and d > 0, the value of \(-\frac{d}{c}\) is positive. Therefore, 1 plus a positive number is positive. a must be greater than 1. a > 1
60- Choice D is correct
\(f(x)=2x^2-5x+1,g(x)=-3x^2-6x+4\)
\((f-g)(x)=f(x)-g(x)=(2x^2-5x+1)-(-3x^2-6x+4)=(2x^2+3x^2 )+(-5x+6x)+(1-4)=5x^2+x-3\)
The Best Books to Ace the CLEP College Mathematics Test
Related to This Article
More math articles
- TASC Math FREE Sample Practice Questions
- 7th Grade OSTP Math Worksheets: FREE & Printable
- FREE 6th Grade PARCC Math Practice Test
- 4th Grade Common Core Math Worksheets: FREE & Printable
- The Ultimate CLEP College Math Formula Cheat Sheet
- How to Solve Parallel Lines and Transversals Problems? (+FREE Worksheet!)
- Full-Length TABE 11 & 12 Math Practice Test-Answers and Explanations
- The Complete Guide to 5 Best GED Math Study Guides
- FREE SSAT Lower Level Math Practice Test
- Volume Calculation Method of Cross-Sections
What people say about "Full-Length CLEP College Mathematics Practice Test-Answers and Explanations - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.