FREE 8th Grade FSA Math Practice Test

Welcome to our FREE 8th Grade FSA Math practice test, with answer key and answer explanations. This practice test’s realistic format and high-quality practice questions can help your student succeed on the FSA Math test. Not only does the test closely match what students will see on the real FSA, but it also comes with detailed answer explanations.

For this practice test, we’ve selected 20 real questions from past exams for your student’s FSA Practice test. Your student will have the chance to try out the most common FSA Math questions. For every question, there is an in-depth explanation of how to solve the question and how to avoid mistakes next time.

Use our free FSA Math practice tests and study resources (updated for 2021) to help your students ace the FSA Math test! Make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions students need to practice.

The Absolute Best Book to Ace 8th Grade FSA Math Test

10 Sample 8th Grade FSA Math Practice Questions

1- What is the slope of a line that is perpendicular to the line
\(4x-2y=12\) ?

A. 2

B. 1

C. \(-2\)

D. \(-\frac{1}{2}\)

2- The diagonal of a rectangle is 10 inches long and the height of the rectangle is 8 inches. What is the perimeter of the rectangle in inches?

3- You can buy 5 cans of green beans at a supermarket for $3.40. How much does it cost to buy 35 cans of green beans?

A. $17

B. $23.80

C. $34.00

D. $119

4- Which of the following is the solution of the following inequality?
\(2x+4>11x-12.5-3.5x\)

A. \(x<3\)

B. \(x>3\)

C. \(x≤4\)

D. \(x≥4\)

5- What is the perimeter of a square that has an area of 595.36 feet?

6- A tree 32 feet tall casts a shadow 12 feet long. Jack is 6 feet tall. How long is Jack’s shadow?

A. 2.25 ft

B. 4 ft

C. 4.25 ft

D. 8 ft

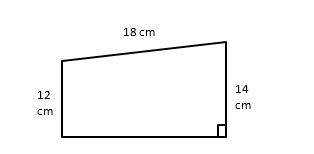
7- The perimeter of the trapezoid below is 54 cm. What is its area?

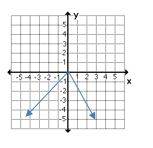
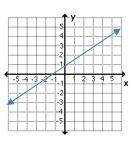
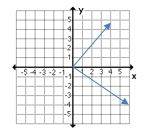
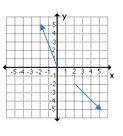
8- Which graph does not represent \(y\) as a function of \(x\)?

A.

B.

C.

D.

9- Which of the following is equivalent to \(13<-3x-2<22\) ?

A. \( -8 < x < -5\)

B. \( 5 < x < 8\)

C. \(\frac{11}{3} < x < \frac{20}{3}\)

D. \(\frac{-20}{3} < x < \frac{-11}{3}\)

10- In a certain bookshelf of a library, there are 35 biology books, 95 history books, and 80 language books. What is the ratio of the number of biology books to the total number of books in this bookshelf?

A. \(\frac{1}{4}\)

B. \(\frac{1}{6}\)

C. \(\frac{2}{7}\)

D. \(\frac{3}{8}\)

11- A bank is offering \(3.5\%\) simple interest on a savings account. If you deposit $12,000, how much interest will you earn in two years?

A. $420

B. $840

C. $4200

D. $8400

12- The area of a circle is \(64 π\). What is the circumference of the circle?

A. \(8 π\)

B. \(16 π\)

C. \(32 π\)

D. \(64 π\)

13- A shirt costing $200 is discounted \(15\%\). After a month, the shirt is discounted another \(15\%\). Which of the following expressions can be used to find the selling price of the shirt?

A. \((200) (0.70)\)

B. \((200) – 200 (0.30)\)

C. \((200) (0.15) – (200) (0.15)\)

D. \((200) (0.85) (0.85)\)

14- Joe scored 20 out of 25 marks in Algebra, 30 out of 40 marks in science, and 68 out of 80 marks in mathematics. In which subject his percentage of marks is best?

A. Algebra

B. Science

C. Mathematics

D. Algebra and Science

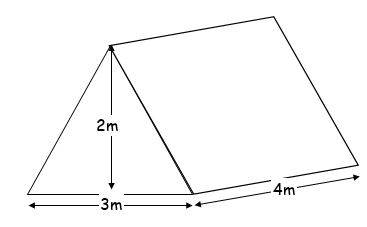
15- What is the volume of the following triangular prism?

16- The marked price of a computer is D dollar. Its price decreased by \(20\%\) in January and later increased by \(10\%\) in February. What is the final price of the computer in D dollars?

A. 0.80 D

B. 0.88 D

C. 0.90 D

D. 1.20 D

17- Triangle ABC is graphed on a coordinate grid with vertices at A \((–3, –2)\), B \((–1, 4)\) and C \((7, 9)\). Triangle ABC is reflected over\( x\) axes to create triangles A’ B’ C’.
Which order pair represents the coordinate of C’?

A. \((7, 9)\)

B. \((–7, –9)\)

C. \((–7, 9)\)

D. \((7, –9)\)

18-

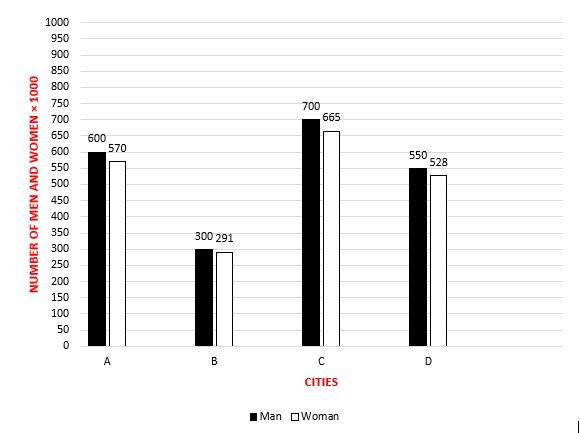
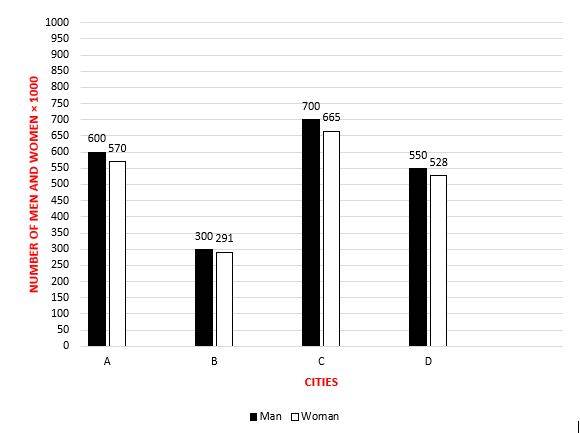
What’s the maximum ratio of women to men in the four cities?

A. 0.98

B. 0.97

C. 0.96

D. 0.95

19-

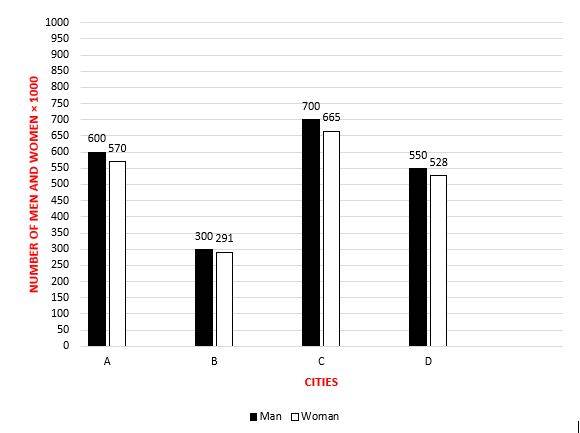
What’s the ratio of the percentage of men in City A to the percentage of women in City C?

A. 0.9

B. 0.95

C. 1

D. 1.05

20-

A container holds 3.5 gallons of water when it is \(\frac{7}{24}\) full. How many gallons of water does the container hold when it’s full?

A. 8

B. 12

C. 16

D. 20

Best 8th Grade FSA Math Prep Resource for 2024

Answers:

2- 28

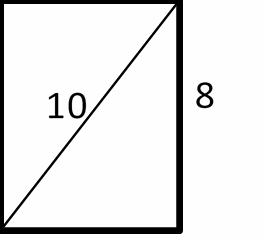
Let\( x\) be the width of the rectangle. Use Pythagorean Theorem:
\(a^2 + b^2 = c^2\)
\(x^2 + 8^2 = 10^2 {\Rightarrow} x^2 + 64 = 100 {\Rightarrow} x^2 = 100 – 64 = 36 ⇒ x = 6\)
Perimeter of the rectangle =\( 2 (length + width) = 2 (8 + 6) = 2 (14) = 28\)

3- B
Let \(x\) be the number of cans. Write the proportion and solve for \(x\).
\(\frac{5 \space cans}{$ 3.40}=\frac{35 \space cans}{x}\)
\(x =\frac{3.40×35}{5}⇒x=$23.8\)

4- A
\(2x+4>11x-12.5-3.5x\)→ Combine like terms:
\(2x+4>7.5x-12.5→\) Subtract \(2x\) from both sides: \(4>5.5x-12.5\)
Add 12.5 both sides of the inequality.
\(16.5>5.5x, \)
Divide both sides by 5.5.
\(\frac{16.5}{5}>x→x<3\)

5- 97.6
Area of a square: \(S = a^2 ⇒ 595.36 = a^2 ⇒ a = 24.4\)
Perimeter of a square: \(P = 4a ⇒ P = 4 × 24.4 ⇒ P = 97.6\)

6- A
Write the proportion and solve for the missing number.
\(\frac{32}{12}=\frac{6}{x}→ 32x=6×12=72 \)
\(32x=72→x=\frac{72}{32}=2.25\)

7- 130
The perimeter of the trapezoid is 54 cm.
Therefore, the missing side (high) is \( 54 – 18 – 12 – 14 = 10\)
Area of a trapezoid: \(A = \frac{1}{2} h (b_1 + b_2) = \frac{1}{2} (10) (12 + 14) = 130\)

8- C
A graph represents \(y\) as a function of \(x\) if
\(x_1=x_2→y_1=y_2 \)
In choice C, for each \(x\), we have two different values for \(y\).

9- A
\(13<-3x-2<22\)→ Add 2 to all sides. \(13+2<-3x-2+2<22+2\)
\(→15<-3x<24\)→ Divide all sides by \(- 3\). (Remember that when you divide all sides of an inequality by a negative number, the inequality sign will be swapped. < becomes >)
\(\frac{15}{-3} > \frac{-3x}{3} >\frac{24}{-3} \)
\(-8 < x < -5\)

10- B
Number of biology books: 35
Total number of books; \(35+95+80=210\)
The ratio of the number of biology books to the total number of books is: \(\frac{35}{210}=\frac{1}{6}\)

11- B
Use a simple interest formula:
I=prt
(I = interest, p = principal, r = rate, t = time)
\(I=(12000)(0.035)(2)=840\)

12- B
Use the formula for the area of circles.
Area \(= πr^2 ⇒ 64 π = πr^2 ⇒ 64 = r^2 ⇒ r = 8\)
The radius of the circle is 8. Now, use the circumference formula:
Circumference\( = 2πr = 2π (8) = 16 π\)

13- D
To find the discount, multiply the number by (\(100\% –\) rate of discount).
Therefore, for the first discount we get: \((200) (100\% – 15\%) = (200) (0.85)\)
For the next \(15\%\) discount: \((200) (0.85) (0.85)\)

14- C
Compare each mark:
In Algebra Joe scored 20 out of 25 in Algebra. It means Joe scored \(80\%\) of the total mark.
\(\frac{20}{25}=\frac{x}{100}⇒x= 80%\)
Joe scored 30 out of 40 in science. It means Joe scored \(75\%\) of the total mark.
\(\frac{30}{40}=\frac{x}{100}⇒x= 75%\)
Joe scored 68 out of 80 in mathematics which means \(85\%\) of the total mark.
\(\frac{68}{80}=\frac{x}{100}⇒x= 85%\)
Therefore, his score in mathematics is higher than his other scores.

15- 12
Use the volume of the triangular prism formula.
\(V =\frac{1}{2} (length) (base) (high)\)
\(V = \frac{1}{2} × 4 × 3 × 2 ⇒ V = 12 \space m^3\)

16- B
To find the discount, multiply the price by (\(100\% –\) rate of discount).
Therefore, for the first discount we get: \((D) (100\% – 20\%) = (D) (0.80) = 0.80 D\)
To increase the \(10 \%: (0.80 D) (100\% + 10\%) = (0.85 D) (1.10) = 0.88 D = 88\%\) of \(D\)

17- D
When a point is reflected over \(x\) axes, the \((y)\) coordinate of that point changes to \((-y)\) while its \(x\) coordinate remains the same.
\(C (7, 9) → C’ (7, -9)\)

18- B
Ratio of women to men in city A: \(\frac{570}{600}=0.95\)
Ratio of women to men in city B: \(\frac{291}{300}=0.97 \)
Ratio of women to men in city C: \(\frac{665}{700}=0.95\)
Ratio of women to men in city D: \(\frac{528}{550}=0.96 \)

19- D
Percentage of men in city \(A = \frac{600}{1170}×100=51.28% \)
Percentage of women in city \(C = \frac{665}{1365}×100=48.72% \)
Percentage of men in city \(A\) to percentage of women in city \(C =\frac{51.28}{48.72}=1.05 \)

20- B
let \(x\) be the number of gallons of water the container holds when it is full.
Then;\(\frac{7}{24}x=3.5→x=\frac{24×3.5}{7}=12\)

Looking for the best resource to help you succeed on the FSA Math test?

The Best Books to Ace the FSA Math Test