FREE 7th Grade PARCC Math Practice Test

The Absolute Best Book to Ace the 7th Grade PARCC Math Test

Common Core Math Exercise Book for Grade 7 Student Workbook and Two Realistic Common Core Math Tests

Download

$29.99 Original price was: $29.99.$16.99Current price is: $16.99.

Rated 4.15 out of 5 based on 40 customer ratings

Satisfied 30 Students

10 Sample 7th Grade PARCC Math Practice Questions

1- What is the slope of a line that is perpendicular to the line \(4x-2y=12\)?

A. \(-2\)

B. 2

C. 4

D. 12

2- Simplify: \(5(x-2y)+(2-x)^2 = (5x-10y)+(4-4x+x^2) = x -10y +4 +x^2\)
When \(x=3\) and \(y=-2\),therefore:
\(x -10y +4 +x^2 =3+20+4+9 =36\)

A. \(-4\)

B. 20

C. 36

D. 50

3- The mean of 50 test scores was calculated as 88. But, it turned out that one of the scores was misread as 94 but it was 69. What is the mean?

A. 85

B. 87

C. 87.5

D. 88.5

4- The width of a box is one third of its length. The height of the box is one third of its width. If the length of the box is 27 cm, what is the volume of the box?

A. 81 cm\(^3\)

B. 162 cm\(^3\)

C. 243 cm\(^3\)

D. 729 cm\(^3\)

5- In five successive hours, a car travels 40 km, 45 km, 50 km, 35 km and 55 km. In the next five hours, it travels with an average speed of 50 km per hour. Find the total distance the car traveled in 10 hours.

A. 425 km

B. 450 km

C. 475 km

D. 500 km

6- The ratio of boys to girls in a school is 2:3. If there are 600 students in a school, how many boys are in the school.____________

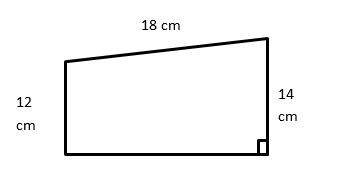
7- The perimeter of the trapezoid below is 54 cm. What is its area? _________

8- In 1999, the average worker’s income increased $2,000 per year starting from $24,000 annual salary. Which equation represents income greater than average? (\(I =\) income, \(x = \)number of years after 1999)

A. \(I > 2000 x + 24000\)

B. \(I > -2000 x + 24000\)

C. \(I < -2000 x + 24000\)

D. \(I < 2000 x – 24000\)

9- Which of the following graphs represents the compound inequality?

A. graph 1

B. graph 2

C. graph 3

D. graph 4

10- A football team had $20,000 to spend on supplies. The team spent $14,000 on new balls. New sport shoes cost $120 each. Which of the following inequalities represent how many new shoes the team can purchase.

A. \( 120x+14,000 ≤20,000 \)

B. \(120x+14,000 ≥20,000\)

C. \(14,000x+12,0 ≤20,000 \)

D. \( 14,000x+12,0 ≥20,000 \)

11- Two dice are thrown simultaneously, what is the probability of getting a sum of 6 or 9?

A. \(\frac{1}{3}\)

B. \(\frac{1}{4}\)

C. \(\frac{1}{6}\)

D. \(\frac{11}{36}\)

12- A swimming pool holds 2,000 cubic feet of water. The swimming pool is 25 feet long and 10 feet wide. How deep is the swimming pool? __________

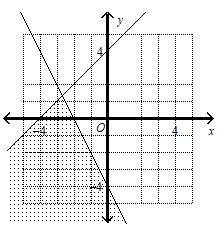
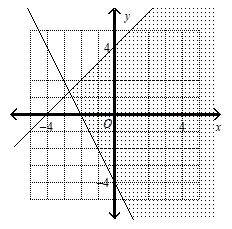
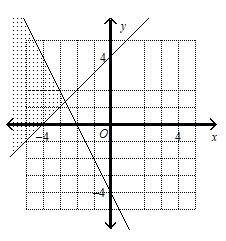
13- Which graph corresponds to the following inequalities?
\(y≤ x + 4\)
\(2x + y ≤ – 4\)

A.

B.

C.

D.

14- A bank is offering \(4.5\%\) simple interest on a savings account. If you deposit $8,000, how much interest will you earn in five years?

A. $360

B. $720

C. $1800

D. $3600

15- A card is drawn at random from a standard 52–card deck, what is the probability that the card is of Hearts? (The deck includes 13 of each suit clubs, diamonds, hearts, and spades)

A. \(\frac{1}{3}\)

B. \(\frac{1}{4}\)

C. \(\frac{1}{6}\)

D. \(\frac{1}{52}\)

16- How long does a 420–miles trip take moving at 50 miles per hour (mph)?

A. 4 hours

B. 6 hours and 24 minutes

C. 8 hours and 24 minutes

D. 8 hours and 30 minutes

17- 11 yards 6 feet and 4 inches equals to how many inches?

A. 388

B. 468

C. 472

D. 476

18- A shirt costing $200 is discounted \(15\%\). After a month, the shirt is discounted another \(15\%\). Which of the following expressions can be used to find the selling price of the shirt?

A. \((200) (0.70)\)

B. \((200) – 200 (0.30)\)

C. \((200) (0.15) – (200) (0.15)\)

D. \((200) (0.85) (0.85)\)

19- Which of the following points lies on the line \(2x + 4y = 10\)

A. \((2, 1)\)

B. \((–1, 3)\)

C. \((–2, 2)\)

D. \((2, 2)\)

20- \(5 + 8 × (–2) – [4 + 22 ×5] ÷ 6 = \)?

A. \(-30\)

B. \(-20\)

C. \(-10\)

D. 0

Best 7th Grade PARCC Math Workbook Resource for 2026

Common Core Mathematics Workbook For Grade 7 Step-By-Step Guide to Preparing for the Common Core Math Test 2019

Download

$29.99 Original price was: $29.99.$16.99Current price is: $16.99.

Rated 4.40 out of 5 based on 144 customer ratings

Satisfied 131 Students

Answers:

2- C
Simplify: \(5(x-2y)+(2-x)^2 = (5x-10y)+(4-4x+x^2) = x -10y +4 +x^2\)
When \(x=3\) and \(y=-2\),therefore:
\(x -10y +4 +x^2 =3+20+4+9 =36\)

3- C
\(average (mean) = \frac{sum \space of \space terms }{number \space of \space terms}⇒ 88 = \frac{sum \space of \space terms}{50}⇒ sum = 88 × 50 = 4400\)
The difference of 94 and 69 is 25. Therefore, 25 should be subtracted from the sum.
\(4400 – 25 = 4375\)
\(mean =\frac{sum \space of \space terms}{number \space of \space terms}⇒ mean = \frac{4375 }{50}= 87.5\)

4- D
If the length of the box is 27, then the width of the box is one third of it, 9, and the height of the box is 3 (one third of the width). The volume of the box is:
\(V = lwh = (27) (9) (3) = 729\)

5- C
Add the first 5 numbers. \(40 + 45 + 50 + 35 + 55 = 225\)
To find the distance traveled in the next 5 hours, multiply the average by number of hours.
\(Distance = Average × Rate = 50 × 5 = 250\)
Add both numbers.
\(250 + 225 = 475\)

6- 240
The ratio of boy to girls is 2:3. Therefore, there are 2 boys out of 5 students. To find the answer, first divide the total number of students by 5, then multiply the result by 2.
\(600 ÷ 5 = 120 ⇒ 120 × 2 = 240\)

7- 130
The perimeter of the trapezoid is 54 cm.
Therefore, the missing side (high) is \(= 54 – 18 – 12 – 14 = 10\)
Area of a trapezoid:
\( A = \frac{1}{2}h (b_1 + b_2) = \frac{1}{2}(10) (12 + 14) = 130\)

8- A
Let \(x\) be the number of years. Therefore, $2,000 per year equals 2000\(x\).
starting from $24,000 annual salary means you should add that amount to 2000\(x\).
Income more than that is:
\(I > 2000x + 24000\)

9- D
Solve for \(x\).
\(-2≤2x-4<8 \)⇒ (add 4 all sides)\( -2+4≤2x-4+4<8+4 \)
\(⇒ 2≤2x<12 \)
⇒ (divide all sides by 2)\( 1≤x<6\)
\(x\) is between 1 and 6.

10- A
Let \(x\) be the number of new shoes the team can purchase. Therefore, the team can purchase 120 \(x\).
The team had $20,000 and spent $14000. Now the team can spend on new shoes $6000 at most.
Now, write the inequality:
\(120x+14.000 ≤20.000\)

11- B
For Sum 6: (1 & 5) and (5 & 1), (2 & 4) and (4 & 2), (3 & 3), so we have 5 options.
For sum 9: (3 & 6) and (6 & 3), (4 & 5) and (5 & 4), we have 4 options.
To get a sum of 6 or 9 for two dice: \(5+4=9\)
Since we have \(6 × 6 = 36\) total options, the probability of getting a sum of 6 and 9 is 9 out of 36 or \(\frac{1}{4}\).

12- 8
Use formula of rectangle prism volume.
\(V = (length) (width) (height) ⇒ 2000 = (25) (10) (height)\)
\( ⇒ height = 2000 ÷ 250 = 8\)

13- A
For each option, choose a point in the solution part and check it on both inequalities.
A. Point \((–4, –4)\) is in the solution section. Let’s check the point in both inequalities.
\(-4 ≤ – 4 + 4, \space It \space works\)
\(2 (–4) + (–4) ≤ –4 ⇒ – 12 ≤ – 4\) it works (this point works in both)
B. Let’s choose this point \((0, 0)\)
\(0 ≤ 0 + 4, \space It \space works\)
\(2 (0) + (0) ≤ –4, \space \space That’s \space not \space true!\)
C. Let’s choose this point \((–5, 0)\)
\(0 ≤ -5 + 4, \space That’s \space not \space true!\)
D. Let’s choose this point \((0, 5)\)
\(5 ≤ 0 + 4, \space That’s \space not \space true!\)

14- C
Use simple interest formula:
I=prt
(I = interest, p = principal, r = rate, t = time)
\(I=(8000)(0.045)(5)=1800\)

15- B
The probability of choosing a Hearts is \(\frac{13}{52}=\frac{1}{4}\)

16- C
Use distance formula:
\(Distance = Rate × time ⇒ 420 = 50 × T\)
divide both sides by 50.
\(\frac{420}{50} = T ⇒ T = 8.4 \space hours\)
Change hours to minutes for the decimal part.
\(0.4 \space hours = 0.4 × 60 = 24 \space minutes\)

17- C
\(11 × 36 + 6 × 12 + 4 = 472\)

18- D
To find the discount, multiply the number by (\(100\% – \)rate of discount).
Therefore, for the first discount we get:
\((200) (100\% – 15\%) = (200) (0.85) = 170\)
For the next \(15%\) discount: \((200) (0.85) (0.85)\)

19- B
Input \((-1, 3)\) in the \(2x + 4y = 10\) formula instead of \(x\) and y. So we have:
\( 2(-1) + 4(3) = 10\)
\(-2 + 12 = 10\)

20- A
Use PEMDAS (order of operation):
\(5 + 8 × (–2) – [4 + 22 ×5] ÷ 6 = 5 + 8 × (–2) – [4 + 110] ÷ 6 = 5 + 8 × (–2) – [114] ÷ 6 = 5 + (–16) – 19 = 5 + (–16) – 19 = –11 – 19 = –30\)

Looking for the best resource to help you succeed on the Grade 7 PARCC Math test?

The Best Books to Ace the 7th Grade PARCC Math Test

Recommended EffortlessMath Books

For more structured prep alongside this practice test, the Common Core Mathematics Workbook for Grade 7 covers every Common Core topic PARCC-style tests assess with worked examples your child can follow on their own. For extra topic-by-topic drills, see the Common Core Math Exercise Book for Grade 7.

Frequently Asked Questions

How many questions were on the 7th Grade PARCC math test?

The original PARCC Grade 7 math test had about 40-50 questions split across 3-4 sessions totaling 110-130 minutes. Many former PARCC states have replaced it since 2019 – New Jersey uses NJSLA, Illinois uses IAR, and several other former PARCC states adopted their own assessments. The question style stayed similar.

Is a calculator allowed on the 7th Grade PARCC math?

Yes, for most sections. PARCC and its successor tests (NJSLA, IAR) allow an on-screen four-function calculator on calculator-allowed items starting in grade 6. A short non-calculator section comes first. Make sure your child still drills fraction-decimal-percent conversions by hand.

What score did kids need to pass the 7th Grade PARCC?

PARCC reported 5 performance levels. Level 4 (“Meets Expectations”) was the on-grade-level target, and Level 5 was “Exceeds Expectations.” Successor tests like NJSLA use the same 5-level structure with similar cutoffs. The scale score range for Grade 7 math was roughly 650-850, with Level 4 starting near 750.

When is the PARCC test given?

PARCC itself was retired by 2019. Successor tests (NJSLA, Illinois IAR) follow the same spring schedule, typically April or May. Your school’s testing coordinator can confirm the dates for whichever state assessment your district now uses.

How was the PARCC Grade 7 math scored?

PARCC math used a scale score (roughly 650-850 at grade 7) with one of 5 performance levels. Multiple-choice and technology-enhanced items were auto-scored; constructed-response items got hand-scored by trained readers. Successor tests follow the same scoring model.

Can my child retake the PARCC?

PARCC itself isn’t given anymore. Successor state tests (NJSLA, IAR) are given once per year in spring with no in-year retake. If your child scored below proficient, the next opportunity is the following spring’s grade-8 test.

What math topics were on the 7th Grade PARCC?

PARCC Grade 7 math covered the Common Core Grade 7 standards: ratios and proportional relationships (unit rates, scale drawings, percent change), the number system (integer and rational number operations), expressions and equations (one- and two-step linear), geometry (angles, area, surface area, volume of prisms, circles), and statistics and probability.

How long should we study for the PARCC or its successor?

About 6-8 weeks of light practice (20-30 minutes a day, 4 days a week) is the sweet spot for grade 7. Start with a diagnostic, focus on the 2-3 weakest topics for the bulk of the time, then finish with full timed practice in the last 1-2 weeks.

Where can I find more PARCC-style practice?

EffortlessMath has free worked-example lessons for every Common Core Grade 7 topic, plus the Common Core Mathematics Workbook for Grade 7 and a Grade 7 word problems book. PARCC-style technology-enhanced items practice well with any Common Core-aligned resource.

Is the PARCC aligned with Common Core?

Yes. PARCC was built explicitly to assess Common Core State Standards. Successor tests like NJSLA and IAR also follow Common Core. Any Common Core Grade 7 math materials work as prep.

Related EffortlessMath Lessons

If a topic on this page feels rusty, these short lessons go deeper:

• Proportional ratios
• How to add and subtract integers
• How to solve one-step equations
• Percent of change
• How to find the volume of a prism