How to Factor Quadratics Using Algebra Tiles

A step-by-step guide to Factoring Quadratics Using Algebra Tiles

One of the visual methods for quadratic factorization is the use of algebra tiles, which can help students understand the factorization process. This method uses physical tiles, each representing a unit square, to represent the terms of a quadratic equation.

To factor an expression like \(ax^2+bx+c\), you must first model the polynomials with tiles and then arrange the tiles in a rectangular or square grid.

A white tile is used for a positive sign and a colored one for a negative one.

Add the \(x^2\) tiles in the upper left corner and the integer tiles in the lower right corner.

Measure the length and width of the square or rectangle formed by counting the tiles and then write it as a linear expression.

The product of the expressions related to length and width is equal to the answer. Check your answer by multiplying these two expressions together.

Note that this method is a visual representation of the factorization process that helps students understand the underlying concepts.

Also, it’s important to note that this method is only useful for quadratic factorization of the form \(ax^2+bx+c\) since that’s the only form that can be represented with algebra tiles.

Factoring Quadratics Using Algebra Tiles-Example 1:

Use algebra tiles to factor: \(x^2+5x+6\).

Solution:

Model the polynomials with tiles:

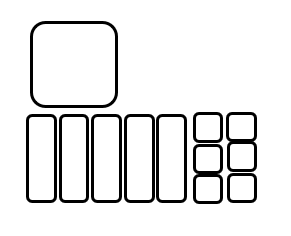
In this case, arrange the tiles into a rectangle grid.

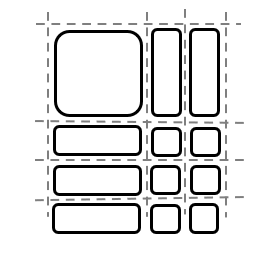
Determine both binomials relate to the divisions, such that \(x+2\) for the horizontal division and \(x+3\) for the vertical. As follow: For education statistics and research, visit the National Center for Education Statistics.

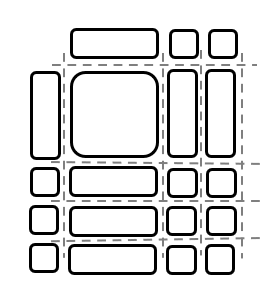
In the end, multiply two expressions and check the answer, For education statistics and research, visit the National Center for Education Statistics.

\((x+2)(x+3)=x^2+5x+6\)