Exterior Angle Theorem

An exterior angle of a triangle is formed when each side of the triangle is drawn. There are \(6\) exterior angles of a triangle each of whose \(3\) sides can be extended on both sides, and \(6\) exterior angles are formed.

Related Topics

• Triangles
• How to Find Complementary, Supplementary, Vertical, Adjacent, and Congruent Angles?

Step by step guide to exterior angle theorem

The exterior angle theorem states that the measure of an exterior angle is equal to the sum of the measures of the two opposite (remote) interior angles of the triangle. Let’s recall some common properties of triangle angles:

• A triangle has \(3\) internal angles which always sum up to \(180\) degrees.
• It has \(6\) exterior angles and this theorem gets applied to each of the exterior angles.

Note that an exterior angle is supplementary to its adjacent interior angle as they form a linear pair of angles. Exterior angles are the angles formed between the side of the polygon and the extended adjacent side of the polygon.

We can confirm the exterior angle theorem with known triangular properties. Consider a \(Δ ABC\).

The three angles \(a + b + c = 180\) ………….. Equation \(1\)

\(c= 180- (a+b)\) ………….. Equation \(2\) (rewriting equation \(1\))

\(e =180- c\) ………….. Equation \(3\) (linear pair of angles)

Substituting the value of \(c\) in equation \(3\), we get

\(e\:=\:180-\left[180-\left(a\:+\:b\right)\right]\)

\(e=180-180+\left(a\:+\:b\right)\)

\(e = a + b\)

Hence verified.

Proof of exterior angle theorem

Consider a \(ΔABC\). \(a, b\) and \(c\) are the angles formed. Extend the side \(BC\) to \(D\). Now an exterior angle \(∠ACD\) is formed. Draw a line \(CE\) parallel to \(AB\). Now \(x\) and \(y\) are the angles formed, where, \(∠ACD = ∠x + ∠y\)

Hence proved that the exterior angle of a triangle is equal to the sum of the two opposite interior angles.

Exterior angle inequality theorem

The exterior angle inequality theorem states that the measure of any exterior angle of a triangle is greater than either of the opposite interior angles. This condition is met by every six external angles of a triangle.

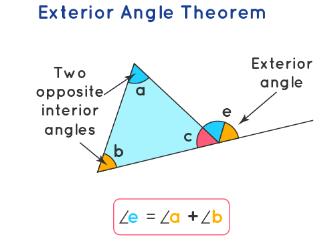
Exterior Angle Theorem – Example 1:

 Find the values of \(x\) and \(y\) by using the exterior angle theorem of a triangle.

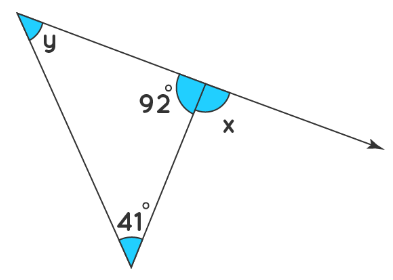
Solution:

\(∠x\) is the exterior angle.

\(∠x + 92 = 180º\) (linear pair of angles)

\(∠x =\:180-92 = 88º\)

Applying the exterior angle theorem, we get, \(∠y + 41 = 88\)

\(∠y = 88-41= 47º\)

Exercises for Exterior Angle Theorem

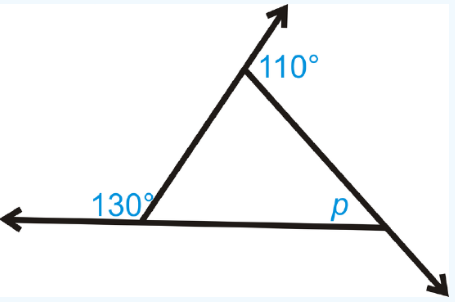
• What is the value of \(p\) in the triangle?

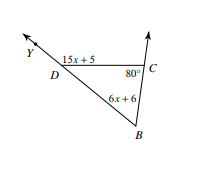
• Find \(m∠YDC\).

• Find \(x\) in the given triangle and then find \(m∠ABD\).

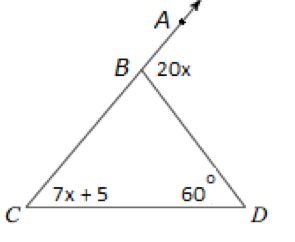
• \(\color{blue}{60^{\circ }}\)
• \(\color{blue}{140^{\circ }}\)
• \(\color{blue}{x=5, m∠ABD = 100^{\circ }}\)