Completing a Table and Make a Graph of Ratios and Rates

There are some equivalent ratios in the ratio table.
Ratio tables are made of two parts (x, y) that follow a certain rule.
The rules may be addition, subtraction, multiplication, or division that repeats in the table.

A step-by-step guide to Completing a Table and Making a Graph of Ratios and Rates

1. Begin by defining the variables and units of measurement for the ratios and rates you will be graphing.
2. Create a table with columns for the variables and rows for the data.
3. Collect and record the data for each variable in the appropriate cells of the table.
4. Calculate the ratios or rates based on the data in the table. These can be expressed as fractions or decimals.
5. Choose an appropriate type of graph to represent the data, such as a bar graph, line graph, or scatter plot.
6. Label the x-axis and y-axis with the appropriate variables and units of measurement.
7. Plot the data points on the graph using the ratios or rates calculated in step 4.
8. Add a title to the graph that clearly describes the data being represented.
9. Finally, analyze the graph and make conclusions about the relationship between the variables.

Ratio Tables – Examples 1

Cups of tomatoes
Cups of hot peppers
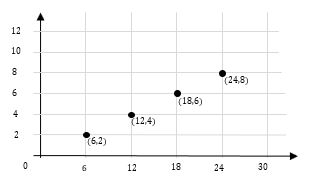
To make the chili sauce, Kate uses 6 cups of tomatoes for every 2 cups of hot peppers. Complete the table and make a graph.

Solutions:
Step 1: Kate uses 6 cups of tomatoes for every 2 cups of hot peppers. So, write it as a rate. \(6÷3=2, 12÷3=4, 18÷3=6, 24÷3=8\)
Step 2: Write them as a ratio. 6:2, 12:4, 18:6, 24:8
Step 3: Make a graph and plot these pairs of ratios on the graph.

Ratio Tables – Examples 2

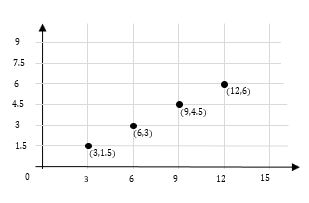
Kevin goes hiking every weekend. He always runs 3 miles lengths at a slow pace for every 1.5-mile length at a fast pace. Complete the table and make a graph.

Solutions:
Step 1: He always runs 3 miles lengths at a slow pace for every 1.5-mile length at a fast pace. So, write it as a rate. \(3÷2=1.5, 6÷2=3, 9÷2=4.5, 12÷2=6\)
Step 2: Write them as a ratio. 3:1.5, 6:3, 9:4.5, 12:6