ASTB Math FREE Sample Practice Questions
Preparing for the ASTB Math test? To succeed on the ASTB Math test, you need to practice as many real ASTB Math questions as possible. There’s nothing like working on ASTB Math sample questions to measure your exam readiness and put you more at ease when taking the ASTB Math test. The sample math questions you’ll find here are brief samples designed to give you the insights you need to be as prepared as possible for your ASTB Math test.
Check out our sample ASTB Math practice questions to find out what areas you need to practice more before taking the ASTB Math test!
Start preparing for the 2022 ASTB Math test with our free sample practice questions. Also, make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions you need to practice.
The Absolute Best Book to Ace the ASTB Math Test
10 Sample ASTB Math Practice Questions
1- Solve the equation: \(log_{4}(x+2) – log_4(x-2) = 1\)
A. 10
B. \(\frac{3}{10}\)
C. \(\frac{10}{3}\)
D. 3
2- Solve: \(e^{(5x + 1 )}= 10 \)
A. \(\frac{ln(10) + 1}{5}\)
B. \(\frac{ln(10) – 1}{5}\)
C. \(5ln (10) + 2\)
D. \(5ln (10) – 2\)
3- If \(f(x) = x – \frac{5}{3}\) and \(f ^{–1}\) is the inverse of \(f(x)\), what is the value of \(f ^{–1(5)\)?
A. \(\frac{10}{3}\)
B. \(\frac{3}{20}\)
C. \(\frac{20}{3}\)
D. \(\frac{3}{10}\)
4- What is cos \(30^{\circ}\)?
A. \(\frac{1}{2}\)
B. \(\frac{{\sqrt{2}}}{2}\)
C. \(\frac{{\sqrt{3}}}{2}\)
D. \(\sqrt{3}\)
5- If \(\theta\) is an acute angle and sin \(\theta = \frac{3}{5}\), then cos \(\theta\) =?
A. \(-1\)
B. 0
C. \(\frac{4}{5}\)
D. \(\frac{5}{4}\)
6- What is the solution of the following system of equations?
\(-2x- y = -9 \)
\(5x-2y= 18\)
A. \((–1, 2)\)
B. \((4, 1)\)
C. \((1, 4)\)
D. \((4, -2)\)
7- Solve.
\(|9 – (12 ÷ | 2 – 5 |)| = \)?
A. 9
B. \(-6\)
C. 5
D. \(-5\)
8- If \(log_{2}x = 5\), then \(x = \)?
A. \(2^{10}\)
B. \(\frac{5}{2}\)
C. \(2^{6}\)
D. 32
9- What’s the reciprocal of \(\frac{x^3}{16}\)?
A. \(\frac{16}{x^3}-1\)
B. \(\frac{48}{x^3}\)
C. \(\frac{16}{x^3}+1\)
D. \(\frac{16}{x^3}\)
10- Find the inverse function for \(ln (2x + 1)\)?
A. \(\frac{1}{2}(e^{x }– 1)\)
B. \((e^{x }+ 1)\)
C. \(\frac{1}{2}(e^{x }+ 1)\)
D. \((e^{x }– 1)\)
Best ASTB Math Prep Resource for 2024
Answers:
1- C
METHOD ONE
\(log_4(x+2) – log_4(x-2) = 1\)
Add \(log_4(x-2)\) to both sides
\(log_4(x+2) – log_4(x-2)+ log_4(x-2)= 1 + log_4(x-2)\)
\(log_4(x+2) = 1 + log_4(x-2)\)
Apply logarithm rule:
\(a = log_b(b^a) ⇒ 1 = log_4(4^1) = log_4(4)\)
then: \(log_4(x+2) = log_4(4) + log_4(x-2)\)
Logarithm rule: \(log_c(a) + log_c(b) = log_c(ab)\)
then: \(log_4(4) + log_4(x-2) = log_4(4(x-2))\)
\(log_4(x+2) = log_4(4(x-2))\)
When the logs have the same base:
\(log_b(f(x)) = log_b(g(x)) ⇒ f(x) = g(x)
(x+2) = 4(x-2)\)
\(x = \frac{10}{3}\)
METHOD TWO
We know that:
\(log_ab-log_ac=log_a\frac{b}{c}\space and \space log_ab=c⇒b=a^c\)
Then: \(log_4(x+2)- log_4(x-2)=log_4\frac{(x + 2)}{(x – 2)}=1⇒\frac{(x + 2)}{(x – 2)}=4^1=4⇒x+2=4(x-2)
⇒x+2=4x-8⇒4x-x=8+2→3x=10⇒x=\frac{10}{3}\)
2- B
\(e^{(5x + 1 )}= 10\)
If \( f(x) = g(x)\), then \(ln(f(x)) = ln(g(x))\)
\(ln(e^{(5x + 1 )})= ln(10)\)
Apply logarithm rule:
\(log_a(x^b) = b log_a(x)\)
\(ln(e^{(5x + 1 )})= (5x + 1)ln(e)\)
\((5x + 1)ln(e) = ln(10)\)
\((5x + 1)ln(e) = (5x + 1)\)
\((5x + 1) = ln(10) \)
\( ⇒x = \frac{ln(10) – 1}{5}\)
3- C
\(f(x) = x –\frac{5}{3}⇒ y = x – \frac{5}{3}⇒ y+ \frac{5}{3}=x\)
\(f^{-1 }= x+ \frac{5}{3}\)
\(f ^{–1}(5) = 5 +\frac{5}{3}=\frac{20}{3}\)
4- C
cos \(30^{\circ} = \frac{\sqrt 3}{2}\)
5- C
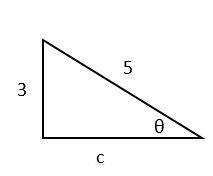
sin\(θ=\frac{3}{5}⇒\) we have following triangle, then:
\(c=\sqrt {(5^2-3^2 )}=\sqrt{(25-9)}=\sqrt 16=4\)
cos\(θ=\frac{4}{5}\)
6- B
\(-2x- y = -9\)
\(5x-2y= 18\)
\(⇒\) Multiplication \((–2)\) in first equation
\(4x +2y =18\)
\(5x-2y= 18\)
Add two equations together \(⇒ 9x =36 ⇒ x= 4\) then: \(y = 1\)
7- C
\(|9 – (12 ÷ | 2 – 5 |)| = |(9-(12÷|-3|))|=|9-(12÷3)|=|9-4|=|5|=5\)
8- D
METHOD ONE
\(log_{2}x = 5\)
Apply logarithm rule: \(a = log_b(b^a)\)
\(5 = log_2(2^5) = log_2(32)\)
\(log_2x = log_2(32)\)
When the logs have the same base: \(log_b(f(x)) = log_b(g(x))⇒ f(x) = g(x)\)
then: \(x = 32\)
METHOD TWO
We know that:
\(log_ab=c⇒b=a^c \)
\(log_2x=5⇒x=2^5=32\)
9- D
\(\frac{x^3}{16}\)
\(⇒\) reciprocal is : \(\frac{16}{x^3}\)
10- A
\(f(x) = ln (2x + 1)\)
\(y = ln (2x + 1)\)
Change variables \(x\) and \(y: x = ln (2y + 1)\)
solve: \(x = ln (2y + 1)\)
\(y = \frac{e^{x}-1}{2}=\frac{1}{2}(e^{x} – 1)\)
The Best Books to Ace the ASTB Math Test
Related to This Article
More math articles
- Full-Length SAT Math Practice Test
- Embarking on an Adventure: How to Solve Word Problems Involving Percents of Numbers and Percent Equations
- How to Add Three or More Fractions with Like Denominators
- The Ultimate 6th Grade TNReady Math Course (+FREE Worksheets)
- How to Solve Word Problems Involving Multiplying Mixed Numbers?
- Full-Length 6th Grade PSSA Math Practice Test-Answers and Explanations
- Top 10 Tips to Overcome ASTB Math Anxiety
- How to Find Mean Absolute Deviation?
- Top 10 SSAT Middle Level Prep Books (Our 2023 Favorite Picks)
- 5th Grade SBAC Math Practice Test Questions
What people say about "ASTB Math FREE Sample Practice Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.