A Complete Explanation of the Continuity over an Interval

Understanding discontinuities and continuity over an interval is a fundamental concept in calculus and mathematical analysis. Let’s delve into each of these topics in detail:

Continuity Over an Interval

Definition: A function is said to be continuous over an interval if it does not have any discontinuities within that interval. This means the function can be drawn without lifting the pen from the paper throughout the interval.

Types of Intervals:

1. Open Interval: An interval \( (a, b) \) is open if it includes all the points between \( a \) and \( b \) but not the endpoints \( a \) and \( b \) themselves.
2. Closed Interval: An interval \([a, b]\) is closed if it includes all the points between \( a \) and \( b \), including the endpoints.
3. Half-Open Interval: An interval that includes one endpoint but not the other, like \( [a, b) \) or \( (a, b] \).

Testing for Continuity:

• To determine if a function is continuous over an interval, one typically checks the continuity at each point in the interval.
• For closed intervals, one also needs to check the left-hand limit at the left endpoint and the right-hand limit at the right endpoint.

Examples:

• Polynomials: Polynomials are continuous over all real numbers, i.e., \((-\infty, \infty)\).
• Rational Functions: Functions like \( \frac{1}{x} \) are continuous everywhere except at points where the denominator is zero.

Discontinuities

Discontinuities occur where a function is not continuous. There are several types:

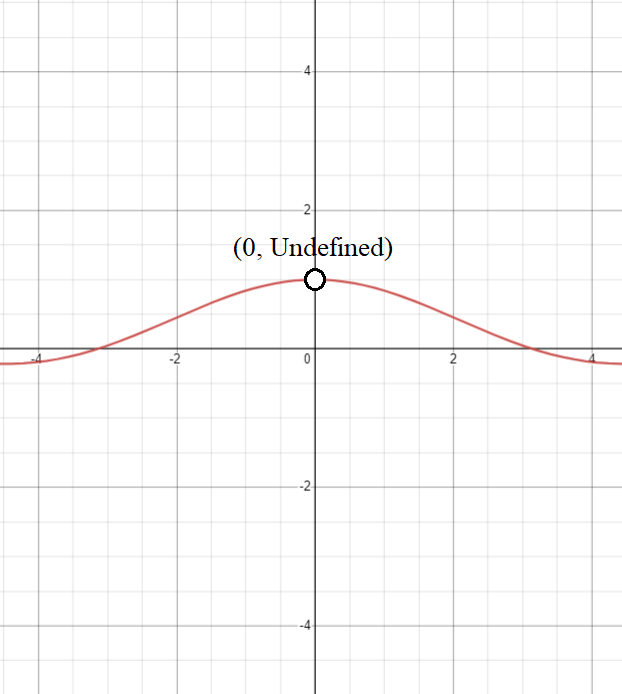
• Point (Removable) Discontinuity: Occurs if a function is not defined at a point, but the limit exists. For example,

\( f(x) = \frac{\sin(x)}{x} \) at \( x = 0 \).

This discontinuity can be “removed” by redefining the function at the point.

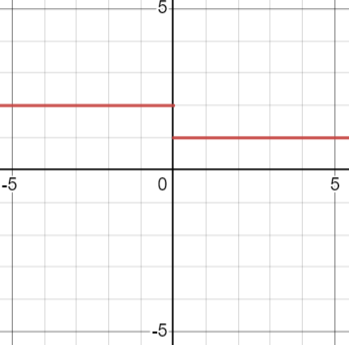
• Jump Discontinuity: This happens when the left and right limits exist at a point but are not equal. For example,

\(f(x) = \begin{cases}
1, & \text{if } x > 0 \\
2, & \text{if } x \leq 0
\end{cases}\)

which jumps from one value to another. This Function is not continuous at \(x=0\)

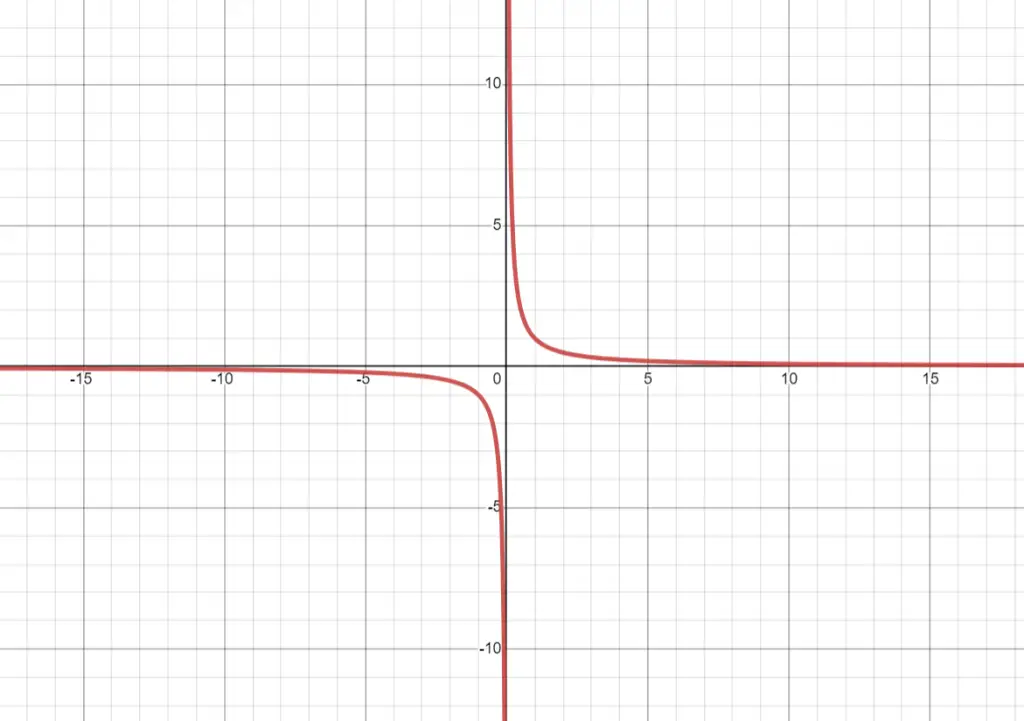
• Infinite Discontinuity: Occurs when the function approaches infinity at a point. A common example is:

\( f(x) = \frac{1}{x} \) at \( x = 0 \).

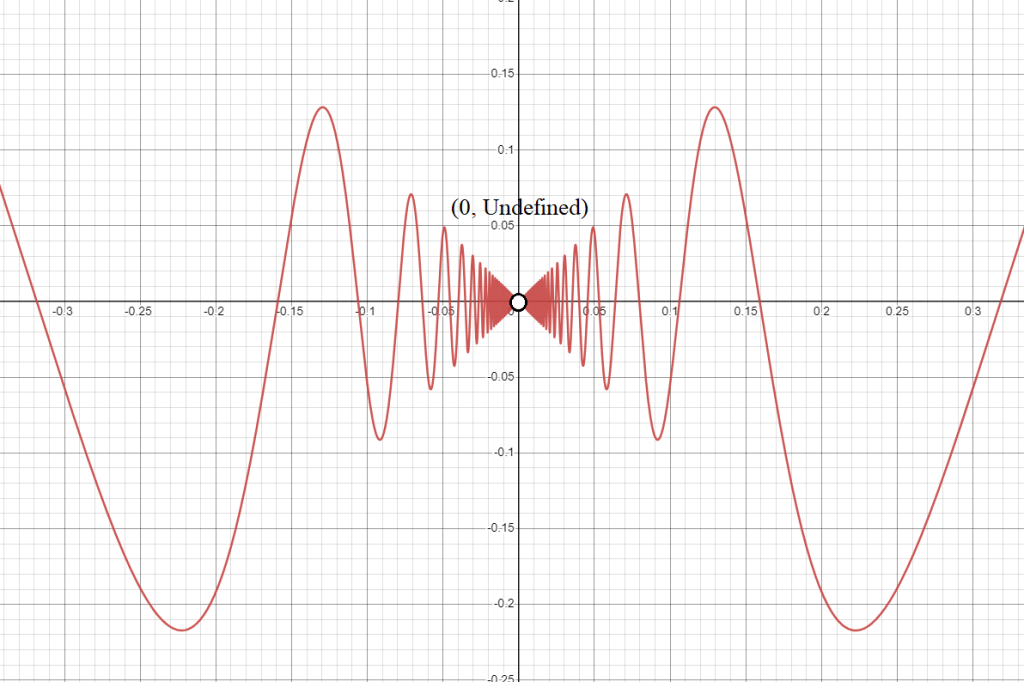
• Oscillating Discontinuity: This is seen in functions that oscillate infinitely near a point, like:

\( f(x) = x\sin(\frac{1}{x}) \) at \( x = 0 \).

Identifying Discontinuities:

• Discontinuities can be identified by looking at the limits and values of a function. If a limit does not exist at a point, or if the limit differs from the function’s value, the function is discontinuous at that point.

Graphical Representation

Graphs of functions are extremely helpful in visualizing continuity and discontinuity. Continuous functions show a smooth curve or line, while discontinuities might appear as breaks, jumps, or vertical asymptotes in the graph.

FAQ

What does it mean for a function to be continuous?

A function is continuous at a point if you can draw the function at that point without lifting your pen. Formally, a function \( f(x) \) is continuous at a point \( x = a \) if the function is defined at \( a \), the limit of \( f(x) \) as \( x \) approaches \( a \) exists, and this limit equals \( f(a) \).

How do you determine if a function is continuous over an interval?

A function is continuous over an interval if it is continuous at every point within that interval. This means checking the function’s behavior at each point, including whether limits exist and match the function’s value at those points.

What are the different types of discontinuities?

The main types of discontinuities are:

• Point (or removable) Discontinuity: The function is not defined at a point, but the limit exists.
• Jump Discontinuity: The left and right limits exist but are not equal.
• Infinite Discontinuity: The function approaches infinity at a point.
• Oscillating Discontinuity: The function oscillates indefinitely near a point.

Can a discontinuity be ‘removed’?

Yes, a point or removable discontinuity can be removed by redefining the function at the point of discontinuity. This is done so that the function’s value at that point matches the limit.

Is a polynomial function always continuous?

Yes, polynomial functions are continuous over the entire set of real numbers, as they do not have any breaks, jumps, or asymptotic behavior.

Why is understanding continuity important?

Understanding continuity is crucial in calculus and mathematical analysis, as it impacts the applicability of various mathematical operations, like integration and differentiation, and is important in fields like physics and engineering.

How do jump and infinite discontinuities differ?

Jump discontinuities occur when a function ‘jumps’ from one value to another, with both left and right limits existing but not equal. Infinite discontinuities occur when the function’s value approaches infinity near a certain point, typically leading to vertical asymptotes on graphs.

What is an example of a function with an oscillating discontinuity?

An example is \( f(x) = \sin(\frac{1}{x}) \) for \( x \neq 0 \). As \( x \) approaches \(zero\), the function oscillates infinitely without settling on a limit.

Are all discontinuities visible on a graph?

Most discontinuities, like jump and infinite discontinuities, are visible on a graph. However, some, like point discontinuities, might not be immediately visible, especially if they’ve been ‘removed’ by redefining the function.

Can a function have more than one type of discontinuity?

Yes, a function can have multiple discontinuities of different types. For instance, a function could have a jump discontinuity at one point and an infinite discontinuity at another.