Using Grid Models to Solve Percentage Problems

To compare a number to 100, you have to use percentages.
The percentage of a number means a ratio between that number and 100.
For instance, 47 percent is the same as:
\(\frac{47}{100}\) (or) 47 to 100 (or) 47:100
Step-by-Step Guide to Using Grid Models to Solve Percentage Problems
- Understand the problem: Read the problem carefully and identify the information provided and the information that needs to be found.
- Draw a grid model: Draw a grid with labeled columns and rows to represent the given and unknown information.
- Identify the part and whole: Identify which quantity represents the part and which represents the whole.
- Write the equation: Write the equation using the information provided in the problem. For example, if the problem states that an item is 20% off, the equation is: (part/whole) = percent/100
- Fill in the grid: Use the information provided in the problem to fill in the grid.
- Solve the equation: Substitute the known values into the equation and solve for the unknown value.
- Check your work: Use the information in the grid to check that the solution makes sense.
- Write the final answer in a complete sentence.
Using Grid Models to Solve Percentage Problems – Examples 1
Problem: A shirt is on sale for 20% off. The original price of the shirt is $40. What is the sale price of the shirt?
- We are given that the shirt is on sale for 20% off and the original price is $40.
- Draw a grid model with labeled columns and rows. Original price, discount, and sale price columns, and whole, percent, and part rows.
- Identify the part and whole: The original price is the whole and the discount is the part.
- Write the equation: (part/whole) = percent/100
- Fill in the grid:
Original price $40 Discount 20% Sale price x
- Solve the equation: (part/whole) = percent/100 => (part/40) = 20/100 => (part) = 8
- Check your work: $40 – $8 = $32, which is the price of the shirt after a 20% discount.
- The sale price of the shirt is $32.
It’s worth noting that this is just one way to use grid models to solve percentage problems, and you can use different models depending on the information provided in the problem.
Using Grid Models to Solve Percentage Problems – Examples 2
In Anne’s library, there are 80 books on the shelves. 20% of those books are short stories. Shade the grid to show the percentage of books that are short stories. And how many books are short stories?
Solutions:
Step 1: The grid is made of 100 equal squares. Since, 20% of the books are short stories, shade 20 of the 100 squares in the grid.
Step 2: To know the number of short stories, you have to multiply the number of all books by the percentage of short stories.
\(80×20%=\frac{80}{1}×\frac{20}{100}=\frac{1600}{100}=16\)
16 books are short stories.

Using Grid Models to Solve Percentage Problems – Examples 3
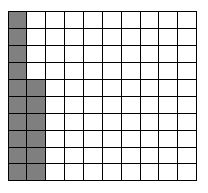
4 of the 25 students at the school got A in an exam. Shade the grid to show the fraction of the students that got an A in an exam. What percent of the students got A on an exam?
Solutions:
Step 1: Since 4 of the 25 students got A in an exam, write it as a fraction: \(\frac{4}{25}\)
Step 2: To know the percentage of the students who got an A in an exam, divide 4 by 25. It is 16%.
Related to This Article
More math articles
- How to Distinguishing Numbers: Prime vs. Composite
- How to Find Integers Equivalent Quotients
- Which Test Is Better for You; GED, TASC, or HiSET? Find Out Now
- Line Graphs
- How to Multiply and Divide Integers? (+FREE Worksheet!)
- 4th Grade OST Math Practice Test Questions
- 5th Grade FSA Math FREE Sample Practice Questions
- Newton’s Technique to Fish Out the Roots
- How Is the CBEST Test Scored?
- What skills Do I need for the GED Math Test?











What people say about "Using Grid Models to Solve Percentage Problems - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.