How to Find Similarity and Ratios? (+FREE Worksheet!)
Two figures are similar if they have the same shape. Learn how to use ratios and proportions to solve similarity problems in a few simple steps.
Related Topics
Step by step guide to solve similarity and ratios problems
- Two or more figures are similar if the corresponding angles are equal, and the corresponding sides are in proportion.
- To solve the similarity problem, you usually need to create a proportion and solve for the unknown side.
The Absolute Best Book to Ace Grade 6 Math
Similarity and Ratios – Example 1:
A girl \(180\) \(cm\) tall, stands \(340\) \(cm\) from a lamp post at night. Her shadow from the light is \(90\) \(cm\) long. How high is the lamp post?
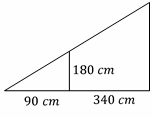
Solution:
Write the proportion and solve for the missing side.
\(\frac{Smaller \ triangle \ height}{Smaller \ triangle \ base} = \frac{Bigger \ triangle \ height}{Bigger \ triangle \ base}\)
\(⇒ \frac{180 \ cm}{90 \ cm }= \frac{x} {90 \ + \ 340 \ cm} ⇒=180 \ × \ 430= 90 × \ x ⇒ 77400= 90 \ x ⇒ x=\frac{77400}{90}=860\) \(cm\)
Similarity and Ratios – Example 2:
A tree \(20\) feet tall casts a shadow \(14\) feet long. Jack is \(10\) feet tall. How long is Jack’s shadow?
Solution:
Write a proportion and solve for the missing number.
\(\frac{20}{14}=\frac{10}{x} → 20 × \ x=10 \ × \ 14\)
\(20 \ x=140→x=\frac{140}{20}=7\)
Similarity and Ratios – Example 3:
A tree\(160\) \(cm\) tall, stands \(360\) \(cm\) from a lamp post at night. Its shadow from the light is \(90\) \(cm\) long. How high is the lamp post?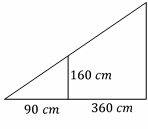
Solution:
Write the proportion and solve for the missing side.
\(\frac{Smaller \ triangle \ height}{Smaller \ triangle \ base}= \frac{Bigger \ triangle \ height}{Bigger \ triangle \ base}\)
\( ⇒ \frac{160 \ cm}{90 \ cm }= \frac{x} {90+360 \ cm} ⇒160×450= 90 × x ⇒ 72000= 90 \ x ⇒ x=\frac{72000}{90}=800\) \(cm\)
The Absolute Best Book to Ace Grade 7 Math
Similarity and Ratios – Example 4:
A tree \(32\) feet tall casts a shadow \(12\) feet long. Jack is \(6\) feet tall. How long is Jack’s shadow?
Solution:
Write a proportion and solve for the missing number.
\( \frac{32}{12}=\frac{6}{x} → 32 × x=6×12\)
\(32x=72→x=\frac{72}{32}=2.25\)
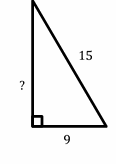
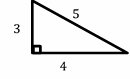
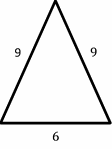
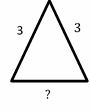
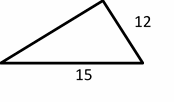
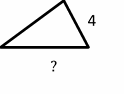
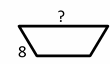
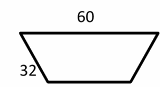
Exercises for Finding Similarity and Ratios
Each pair of figures is similar. Find the missing side.
Download Similarity and Ratios Worksheet
Answers
- \(\color{blue}{9}\)
- \(\color{blue}{2}\)
- \(\color{blue}{5}\)
- \(\color{blue}{15}\)
Best Math for Grade 5 Resource
Related to This Article
More math articles
- 10 Must-Have Elementary Classroom Math Supplies
- 6th Grade KAP Math Worksheets: FREE & Printable
- Top 10 Algebra 1 Books in 2024 (Expert Recommendations)
- What to Look for in Graphing Calculators?
- Unlock the Answers: “GED Math for Beginners” Solution Manual
- 7th Grade ACT Aspire Math FREE Sample Practice Questions
- How to Simplify Ratios? (+FREE Worksheet!)
- Word Problems Involving Money
- Three and A Half Principles of Extraordinary Techniques for Math Teaching
- What if I Fail the CBEST Test?
What people say about "How to Find Similarity and Ratios? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.