Number Patterns for 5th Grade: Sequences and Rules

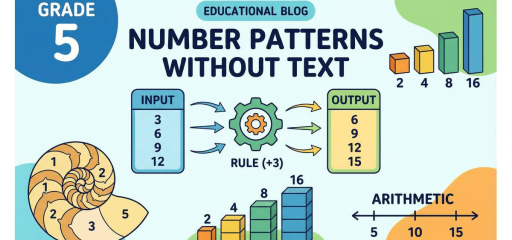
Number patterns are sequences of numbers that follow a rule. In Grade 5, students identify, extend, and create number patterns. Patterns may involve adding or subtracting the same amount each time (arithmetic), multiplying or dividing by the same factor (geometric), or more complex rules. Recognizing patterns helps students make predictions, solve problems efficiently, and develop algebraic thinking.

To find the rule of a pattern, we look at how each number relates to the next. If the difference between consecutive terms is constant, the rule is add or subtract. If the ratio between consecutive terms is constant, the rule is multiply or divide. Once we know the rule, we can extend the pattern to find the next term or any term in the sequence.

DETAILED EXPLANATION

Arithmetic patterns: Same difference between consecutive terms.

• Example: 2, 5, 8, 11, 14. Differences: 3, 3, 3, 3. Rule: add 3. Next: 17.

The Absolute Best Book to Ace Grade 5 Math

The Ultimate Elementary School Math Bundle Grade 3-5

Download

$109.99 Original price was: $109.99.$54.99Current price is: $54.99.

Geometric patterns: Same ratio between consecutive terms.

• Example: 3, 6, 12, 24. Ratios: 6÷3=2, 12÷6=2, 24÷12=2. Rule: multiply by 2. Next: 48.

To find the nth term or a specific term: For arithmetic, if we start at a and add d each time, the terms are a, a+d, a+2d, a+3d, …. For geometric, if we start at a and multiply by r, the terms are a, ar, ar², ar³, ….

WORKED EXAMPLES WITH STEP BY STEP SOLUTIONS

Example 1

Find the next number: 2, 5, 8, 11, 14, ___

Solutions:

Step 1: Find the difference between consecutive terms: \(5 – 2 = 3\), \(8 – 5 = 3\), \(11 – 8 = 3\), \(14 – 11 = 3\).

The Ultimate Middle School Math Bundle: Grades 6 to 8

Step 2: The difference is constant (3). The rule is add 3.

Step 3: Apply the rule: \(14 + 3 = 17\).

Step 4: The next number is 17.

Answer: 17

Example 2

Find the next number: 3, 6, 12, 24, ___

Solutions:

Step 1: Find the ratio between consecutive terms: \(6 \div 3 = 2\), \(12 \div 6 = 2\), \(24 \div 12 = 2\).

Step 2: The ratio is constant (2). The rule is multiply by 2.

Mastering Grade 5 Math

Mastering Grade 5 Math The Ultimate Step by Step Guide to Acing 5th Grade Math

Download

$29.99 Original price was: $29.99.$16.99Current price is: $16.99.

Step 3: Apply the rule: \(24 \times 2 = 48\).

Step 4: The next number is 48.

Answer: 48

Example 3

A pattern starts at 100 and subtracts 7 each time. What is the 5th number?

Solutions:

Step 1: Start at 100. Subtract 7 each time.

Step 2: 1st: 100. 2nd: 100 − 7 = 93. 3rd: 93 − 7 = 86. 4th: 86 − 7 = 79. 5th: 79 − 7 = 72.

Step 3: The 5th number is 72.

Answer: 72

Example 4

Find the next two numbers: 5, 10, 20, 40, ___, ___

Solutions:

Step 1: Check ratios: \(10 \div 5 = 2\), \(20 \div 10 = 2\), \(40 \div 20 = 2\). Rule: multiply by 2.

Step 2: Next: \(40 \times 2 = 80\). Then: \(80 \times 2 = 160\).

Answer: 80, 160