How to Find Constant of Proportionality?

When two variables are directly or indirectly proportional to each other, their relationship can be described as \(y=kx\),  where \(k\) is known as the constant of proportionality.

A step-by-step guide to finding the constant of proportionality

The constant of proportionality is the constant value of the ratio between two proportional quantities. Two varying quantities are said to be in a relation of proportionality when their ratio or product yields a constant. The constant value of proportionality depends on the type of proportion between the two given quantities:

1. Direct variation: The equation of direct proportionality is \(y = kx\), which shows that as \(x\) increases, \(y\) also increases at the same rate. Example: the cost of each item \((y)\) is directly proportional to the number of items \((x)\) purchased, expressed as \(y ∝ x\).
2. Inverse variation: The indirect proportionality equation is \(y= \frac{k}{x}\), which shows that as \(y\) increases, \(x\) decreases and vice versa. Example: the speed of a moving vehicle \((y)\) inversely varies as the time taken \((x)\) to travel a certain distance, expressed as \(y ∝ \frac{1}{x}\).

In both cases, \(k\) is constant. The value of this constant is called the coefficient of proportionality. The constant of proportionality is also known as the unit rate.

Working with proportional relationships allows a person to solve many real-life problems:

• Adjusting the ratio of ingredients in the recipe
• A quantifying chance like finding the odds and probability of events
• Scaling a diagram for design and architectural applications
• Finding percent increase or percent decrease for price mark-ups
• Discount products based on unit rate

How to solve the constant of proportionality?

We apply our knowledge of direct and inverse changes, identify them, and then determine the constant of proportionality, thereby finding solutions to our problems.

For example: Find the constant of proportionality, if \(y=40\) and \(x=4\) and \(y ∝ x\).

Solution: 

We know that \(y\) varies proportionally with \(x\). We can write the equation of the proportional relationship as \(y = kx\). Substitute the given \(x\) and \(y\) values, and solve for \(k\).

\(40 = k (4)\)

\(k = 40 ÷ 4 = 10\)

Therefore, the constant of proportionality is \(10\).

Find Constant of Proportionality – Example 1:

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality. 

Solution : 

First, find the ratio of \(x\) and \(y\) for all the given values. 

\(\frac{2 }{1} = 2\)

\(\frac{4}{2} = 2\)

\(\frac{8}{4} = 2\)

When we take the ratio of \(x\) and \(y\) for all the given values, we get equal values for all the ratios. So, the relationship shown in the table is proportional.   

Exercises for Finding Constants of Proportionality

Examine each table and determine if the relationship is proportional.

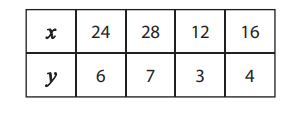
1. \(\color{blue}{Not}\)
2. \(\color{blue}{Yes}\)