Full-Length 7th Grade MCAS Math Practice Test-Answers and Explanations

Did you take the 7th Grade MCAS Math Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.
7th Grade MCAS Math Practice Test Answers and Explanations
1- Choice C is correct.
If the score of Mia was 90, then the score of Ava is 30. Since the score of Emma was one and a half as that of Ava, therefore, the score of Emma is 1.5 × 30 = 45.
2- Choice A is correct
Write the ratio and solve for \(x\).
\( \frac{60}{50}=\frac{5x+2}{10}⇒ 12=5x+2 ⇒12-2=5x⇒ x=\frac{10}{5}=2\)
3- Choice B is correct
Let \(x\) be the number of students in the class. \(40\%\) of \(x\) = girls, \(25\%\) of girls = tennis player,
Find \(25\%\) of \(40\%\). Then: \(25\%\) of \(40\%=0.25×0.40=0.1=10\%\) or \(\frac{10}{100}=\frac{1}{10}\)
4- Choice C is correct
Use the information provided in the question to draw the shape.
Use Pythagorean Theorem: \(a^2+b^2=c^2\)
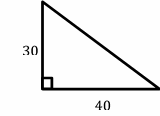
\(30^2+40^2=c^2⇒ 900+1600= c^2⇒2500= c^2⇒c=50\)
5- Choice A is correct
Write a proportion and solve for \(x\).
\( \frac{12 \space Cans}{$ 7.40}=\frac{30 \space Cans}{x }, x= \frac{7.40×30}{12} ⇒x=$18.5\)
6- Choice D is correct
Use the volume of square pyramid formula.
\(V= \frac{1}{3} a^2 h ⇒V=\frac{1}{3} (12 \space m)^2×20 \space m ⇒ V=960 \space m^3\)
7- Choice C is correct
Let \(x\) be the number of soft drinks for 240 guests. Write a proportional ratio to find \(x\). \(\frac{6 \space soft \space drinks}{8 \space guests}=\frac{x}{240 \space guests}, x=\frac{240×6}{8}⇒x=180\)
8- Choice B is correct
Use the formula for Percent of Change: \(\frac{New \space Value-Old \space Value}{Old \space Value}×100\%, \frac{1.75-1.4}{1.4}×100\%=25\%\)
9- The answer is: \(-99\)
Use PEMDAS (order of operation):
\([8×(-14)+15]-(10)+[4×6]÷3=[-122+15]-(10)+8=-97-10+8=-99\)
10- Choice D is correct
Simplify. \(5x^2 y(2xy^3)^4=5x^2 y(16x^4 y^{12} )=80x^6 y^{13}\)
The Absolute Best Book to Ace the 7th Grade MCAS Math Test
Common Core Math Exercise Book for Grade 7 Student Workbook and Two Realistic Common Core Math Tests
11- Choice C is correct
The distance between Jason and Joe is 14 miles. Jason running at 6 miles per hour and Joe is running at the speed of 8 miles per hour. Therefore, every hour the distance is 2 miles less.
14 ÷ 2 = 7
12- Choice A is correct.
Let x be the integer. Then: \(5x-9=101\), Add 9 both sides: \(5x=110\), Divide both sides by 5: \(x=22\)
13- Choice D is correct
Two and half times of 18,000 is 45,000. One-fifth of them canceled their tickets.
One sixth of \(45,000\) equals \(9,000(\frac{1}{5} × 45000=9000)\).
\(36,000(45000-9000=36000)\) fans are attending this week
14- Choice C is correct
Write the numbers in order: \(25,12,13,18,22,36,22\)
Since we have 7 numbers (7 is odd), then the median is the number in the middle, which is 22.
15- Choice D is correct.
The question is: 615 is what percent of 820?
Use percent formula: \(part=\frac{percent}{100}×whole\)
\(615=\frac{percent}{100}×820 ⇒ 615=\frac{percent ×820}{100}⇒61,500=percent×820\) ⇒
\(percent=\frac{61,500}{820}=75\), \(615\) is \(75\%\) of \(820\). Therefore, the discount is: \(100\%-75\%=25\%\)
16- The answer is \(22 \frac{1}{3}\) miles.
Robert runs \(4 \frac{1}{3}\) miles on Saturday and \(2(4 \frac{1}{3})\) miles on Monday and Wednesday.
Robert wants to run a total of 35 miles this week. Therefore, subtract 4 \(\frac{1}{3}+2(4 \frac{1}{3})\) from 35.
\(35-(4 \frac{1}{3}+2(4 \frac{1}{3} ))=35-12 \frac{2}{3}=22 \frac{1}{3}\) miles
17- Choice B is correct
To find the area of the shaded region, find the difference of the area of two circles. \(S_1\): the area of bigger circle. \(S_2\): the area of the smaller circle). Use the area of circle formula. \(S=πr^2\)
\(S_1- S_2=π(6 \space cm)^2- π(4 \space cm)^2⇒S_1- S_2=36π \space cm^2-16π \space cm^2 ⇒ S_1- S_2 =20π \space cm^2\)
18- Choice A is correct
Use Pythagorean Theorem: \(a^2+b^2=c^2\),
\(12^2+5^2=c^2⇒ 144+25= c^2 ⇒ c^2=169 ⇒c=13\)
19- Choice A is correct
Let L be the price of the laptop and C be the price of the computer. 4(L) =7(C) and L = $240 + C
Therefore, 4($240 + C) =7C ⇒ $960 + 4C = 7C ⇒ C=$320
20- The answer is 70.
Jason needs an \(75\%\) average to pass five exams. Therefore, the sum of 5 exams must be at least \(5×75=375\), The sum of 4 exams is \(62+73+82+88=305\).
The minimum score Jason can earn on his fifth and final test to pass is:
\( 375-305=70\)
21- Choice B is correct.
Let \(x\) be the original price. If the price of a laptop is decreased by \(15\%\) to $425, then:
\(85\%\) of \(x=425 ⇒ 0.85x=425 ⇒ x=425÷0.85=500\)
22- Choice C is correct.
The weight of 12 meters of this rope is: \(12×450 \space g=5,400 \space g\)
\(1 \space kg=1,000 \space g\), therefore, \(5,400 \space g÷1,000=5.4 \space kg\)
23- Choice D is correct.
Only option D is correct. Other options don’t work in the equation.
\((4x-2)x=42\)
24- Choice C is correct
Compare each score: In Algebra Joe scored 24 out of 32 in Algebra that it means \(75\%\) of total mark. \(\frac{24}{32}= \frac{x}{100}⇒x=75\)
Joe scored 28 out of 40 in science that it means \(70\%\) of total mark. \(\frac{28}{40}=\frac{x}{100} ⇒x=70\)
Joe scored 72 out of 90 in mathematics that it means \(80\%\) of total mark. \(\frac{72}{90}=\frac{x}{100} ⇒x=80\)
Therefore, his score in mathematics is higher than his other scores.
25- Choice B is correct
To find the discount, multiply the number by (\(100\%\)-rate of discount).
Therefore, for the first discount we get: \((D)(100\%-25\%)=(D)(0.75)=0.75\)
For increase of \(15\%\): \((0.75D)(100\%+15\%)=(0.75D)(1.15)=0.8625 D=86.25\%\) of \(D\)
Best 7th Grade MCAS Math Prep Resource for 2022
26- Choice B is correct
Write the numbers in order: \(42,21,15,28,43,34,26\)
Since we have 7 numbers (7 is odd), then the median is the number in the middle, which is 28.
27- Choice C is correct
The average speed of John is: \(210÷7=30\) km, The average speed of Alice is: \(160÷5=32\) km, Write the ratio and simplify. \(30∶ 32 ⇒ 15∶16\)
28- Choice D is correct
Use the formula for Percent of Change: \(\frac{New \space Value-Old \space Value}{Old \space Value)}×100\%\)
\(\frac{42-56}{56}×100\%=-25\%\) (negative sign here means that the new price is less than old price).
29- Choice C is correct
Use the formula of areas of circles.
Area \(=πr^2 ⇒ 121π= πr^2 ⇒ 121= r^2⇒ r=11\)
Radius of the circle is 11. Now, use the circumference formula:
Circumference \(=2πr=2π(11)=22π\)
30- Choice B is correct.
Let \(x\) be the number of balls. Then: \(\frac{1}{2} x+\frac{1}{5} x+\frac{1}{10} x+12=x\)
\((\frac{1}{2}+\frac{1}{5}+\frac{1}{10})x+12=x, (\frac{8}{10})x+12=x,x=60\), In the bag of small balls \(\frac{1}{5}\) are white, then: \(\frac{60}{5}=12\), There are 12 white balls in the bag.
31-Choice A is correct
William ate \(\frac{4}{5}\) of \(10\) parts of his pizza that it means \(8\) parts out of \(10\) parts \((\frac{4}{5}\) of 10 parts \(=x ⇒ x=8)\) and left \(2\) parts. Ella ate \(\frac{1}{2}\) of 10 parts of her pizza that it means \(5\) parts out of 10 parts \((\frac{1}{2}\) of 10 parts \(= x ⇒ x=5)\) and left \(5\) parts. Therefore, they ate \((5+2)\) parts out of \((10+10)\) parts of their pizza and left \((5+2)\) parts out of \((10 + 10)\) parts of their pizza. It means: \(\frac{7}{20}\), After simplification we have: \(\frac{7}{20}\)
32-Choices D is correct.
The failing rate is \(14\) out of \( 50=\frac{14}{50}\), Change the fraction to percent: \(\frac{14}{50} ×100\%=28\%\)
\(28\) percent of students failed. Therefore, \(72\) percent of students passed the exam.
33-Choice C is correct
\(x\%\) of \(50\) is \(6.2\), then: \( 0.50x=6.2 ⇒x=6.2÷0.50=12.4\)
34-The answer is 56
Use the area of the square formula. \(S=a^2 ⇒ 196= a^2 ⇒ a=14\) One side of the square is 14 feet. Use the perimeter of the square formula. \(P=4a ⇒ P=4(14) ⇒ P=56\)
35-Choice B is correct.
Input the points instead of \(x\) and \(y\) in the formula. Only option B works in the equation.\(6x-14=4y, 4(2)-14=4(-\frac{1}{2})⇒-2=-2\)
36-Choice B is correct.
The sum of supplement angles is 180. Let \(x\) be that angle.
Therefore, \(x+4x=180\)
\(5x=180\), divide both sides by 5: \(x=36\)
37-Choice B is correct.
Use simple interest formula: \(I=prt (I=interest,p=principal,r= rate,t=time) I=(16,000)(0.035)(3)=1,680\)
38-Choice B is correct.
Total number of way is \(6×6=36\).favorable cases is \((1,6),(2,5),(3,4),(4,3),(5,2),(6,1)\). Thus probability that sum of two tice get \(7\) is \(\frac{6}{36}=\frac{1}{6}\)
39-The answer is 168.
To find the number of possible outfit combinations, multiply the number of options for each factor: \(3×8×7=168\)
40-Choice B is correct.
\(7\%\) of the volume of the solution is alcohol. Let \(x\) be the volume of the solution. Then: \(7\%\) of \(x=35 \space ml ⇒ 0.07 x=35 ⇒ x=35 ÷ 0.07=500\)
The Best Books to Ace the 7th Grade MCAS Math Test
Common Core Math Exercise Book for Grade 7 Student Workbook and Two Realistic Common Core Math Tests
Related to This Article
More math articles
- How to Model and Solve Equations Using Algebra Tiles
- How to Use Number Lines for Multiplication by a Negative Integer?
- The Ultimate 7th Grade OAA Math Course (+FREE Worksheets)
- 10 Most Common 4th Grade Common Core Math Questions
- Top 10 7th Grade FSA Math Practice Questions
- Top 10 Tips to Create a TSI Math Study Plan
- The Great Math Tour: Exploring the World of Circle Graphs
- 8th Grade MEAP Math FREE Sample Practice Questions
- Finding Area of Compound Figures
- HiSET Math FREE Sample Practice Questions














What people say about "Full-Length 7th Grade MCAS Math Practice Test-Answers and Explanations - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.