Equation of Each Ellipse and Finding the Foci, Vertices, and Co– Vertices of Ellipses

An Ellipse is a closed curve formed by a plane. There are two types of ellipses: Horizontal and Vertical

• If major axis of an ellipse is parallel to \(x\), its called horizontal ellipse.
• If major axis of an ellipse is parallel to \(y\), its called vertical ellipse.

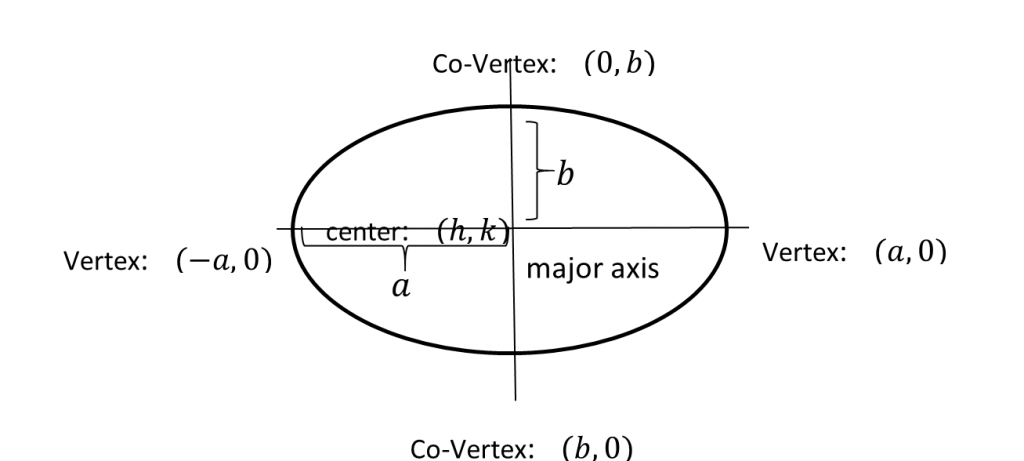
Step by Step Guide to Find Equation of Ellipses

The standard form of the equation of an Ellipse is:

• Horizontal: \(\color{blue}{\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1}\)
• Vertical: \(\color{blue}{\frac{(x-h)^2}{b^2}+\frac{(y-k)^2}{a^2}=1}\)

The center is: \(\color{blue}{(h, k)}\)

The vertices are: \(\color{blue}{(h+a, k), (h-a, k)}\)

The foci are: \(\color{blue}{(h+c, k), (h-c, k)}\), where \(\color{blue}{c=\sqrt{a^2-b^2}}\)

The Values can be calculated according to the standard form of the equation of ellipses.

Equation of Each Ellipse and Finding the Foci, Vertices, and Co– Vertices of Ellipses – Example 1:

Find the center, vertices, and foci of this ellipse: \(\frac{(x-2)^2}{36}+\frac{(y+4)^2}{16}=1\)

Solution:

The standard form of the equation of an Ellipse is: \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\)

Then, \((h=2, k=-4, a=6, b=4)\).

So, the center is \((2, -4)\).

The vertices are \((h+a, k), (h-a, k) →(8, 4), (-4, 4)\)

Evaluate \(c\): \(c=\sqrt{a^2-b^2}\) \(=\sqrt{36-16}=2\sqrt{5}\)

Then the foci are \((2+2\sqrt{5}, -4)\) and \((2-2\sqrt{5}, -4)\).

Exercises for Equation of Finding the Foci, Vertices, and Co– Vertices of Ellipses

Find the center, vertices, and foci of each ellipse.

• \(\color{blue}{9x^2+4y^2=1}\)
• \(\color{blue}{16x^2+25y^2=100}\)
• \(\color{blue}{25x^2+4y^2+100x-40y=400}\)
• \(\color{blue}{\frac{(x-1)^2}{9}+\frac{y^2}{5}=100}\)

• \(\color{blue}{Center: (0, 0), Vertices: (0,\frac{1}{2}), (0, -\frac{1}{2}), foci: (0, \frac{\sqrt{5}}{6}), (0, -\frac{\sqrt{5}}{6})}\)
• \(\color{blue}{Center: (0, 0), Vertices: (\frac{5}{2}, 0), (-\frac{5}{2}, 0), foci: (\frac{3}{2}, 0), (-\frac{3}{2}, 0)}\)
• \(\color{blue}{Center: (-2, 5), Vertices: (-2,5+5\sqrt{6}), (-2, 5-5\sqrt{6}), foci: (-2, 5+3\sqrt{14}), (-2, 5-3\sqrt{14})}\)
• \(\color{blue}{Center: (1, 0), Vertices: (31, 0), (-29, 0), foci: (21, 0), (-19, 0)}\)