Count Lines of Symmetry
Do you know how many lines of symmetry each shape has and how can they be identified? Join us in this article to answer these questions.

Whenever a line separates a particular figure into \(2\) equivalent halves so the right and left halves match precisely, then we declare the figure is symmetrical regarding the line. This line is known as the line of symmetry or the axis of symmetry.
Related Topics
For the particular regular polygons, you can locate the lines of symmetry via utilizing a paper folding technique as well as additionally create the lines of symmetry using dotted lines.
Shapes with Line Symmetry
A few of the commonplace instances of line symmetry are shown below:
- Squares have four lines of symmetry, which are lines going through the opposing vertices along with the lines through the midpoints of opposing sides making up the \(4\) lines of symmetry.
- Rectangles have \(2\) two lines of symmetry, which are lines through the midpoints of the opposing sides.
- Generic trapezoids will not have line symmetry rather isosceles trapezoids have line symmetry.
Count Lines of Symmetry – Example 1:
Draw lines of symmetry on the shape. Count and write the lines of symmetry you see.
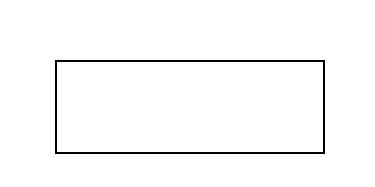
Solution:
As mentioned, a rectangle has \(2\) two lines of symmetry, which are lines through the midpoints of the opposing sides.
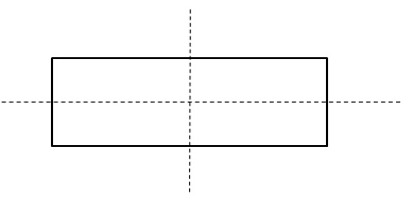
Count Lines of Symmetry – Example 2:
Draw lines of symmetry on the shape. Count and write the lines of symmetry you see.
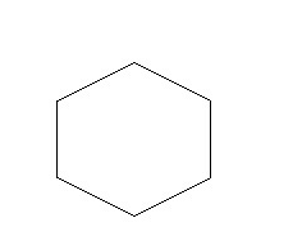
Solution:
The figure above is a hexagon. A hexagon has \(6\) lines of symmetry because in regular polygons the number of lines of symmetry is equal to the number of sides
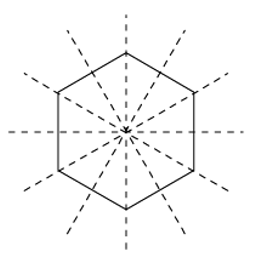
Exercises for Count Lines of Symmetry
Draw lines of symmetry on each shape.
1)
2)

1)
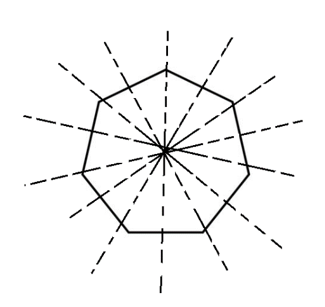
2)
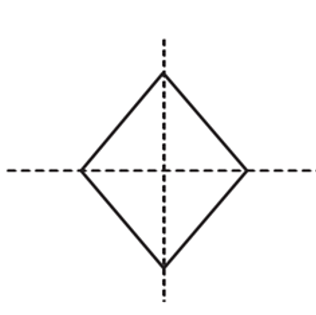
Related to This Article
More math articles
- 3rd Grade OSTP Math Worksheets: FREE & Printable
- FREE 6th Grade ACT Aspire Math Practice Test
- FREE 6th Grade Common Core Math Practice Test
- 4th Grade SBAC Math Worksheets: FREE & Printable
- Gain Access to the Answers: Explore the Solution Manual for “CHSPE Math for Beginners”
- How to Apply Integers Multiplication and Division Rules?
- 10 Most Common 6th Grade MEAP Math Questions
- How to Find Mean Absolute Deviation?
- FREE TABE Math Practice Test
- How to Find Elapsed Time?



















What people say about "Count Lines of Symmetry - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.