How to Find the Volume and Surface Area of a Triangular Pyramid?

A three-dimensional shape whose four sides are triangular is known as a triangular pyramid. Triangular pyramids are irregular, regular, and right-angled.

Related Topics

• How to Find the Surface Area of a Pyramid?

A step-by-step guide to finding the volume and surface area of the triangular pyramid

A triangular pyramid is a three-dimensional shape in which all faces are triangular. It is a pyramid with a triangular base connected by four triangular faces in which \(3\) faces meet at a vertex. If it is a right triangular pyramid, the base is a right-angled triangle and the other sides of the triangle are isosceles.

Types of the triangular pyramid

Like any other geometric shape, triangular pyramids can be classified into regular and irregular pyramids.

Regular triangular pyramid

A regular triangular pyramid has equilateral triangles. Since it is made of equilateral triangles, its interior angles are \(60\) degrees.

Irregular triangular pyramid

Irregular triangular pyramids also have triangular faces, but they are not equilateral. The internal angles in each plane add up to \(180°\) due to the triangle. Unless a triangular pyramid is mentioned explicitly as irregular, all triangular pyramids are assumed to be regular triangular pyramids.

Right triangular pyramid

The right triangular pyramid has the base of the right triangle and its apex is located above the center of the base. It has \(1\) right-angled base, \(6\) edges, \(3\) triangular faces, and \(4\) vertices.

Properties of a triangular pyramid

A triangular pyramid feature helps us identify a pyramid from a set of specific shapes quickly and easily. The different properties of a triangular pyramid are:

• A triangular pyramid has \(4\) triangular faces, \(6\) edges, and \(4\) vertices.
• \(3\) edges meet at each of its vertexes.
• A triangular pyramid has no parallel faces.
• A regular triangular pyramid has equilateral triangles for all its faces. It has \(6\) planes of symmetry.
• Triangular pyramids can be regular, irregular, and right-angled.

Triangular pyramid formulas

There are various formulas used to calculate the volume and area of triangular pyramids. See the following figure to relate to the formulas given below:

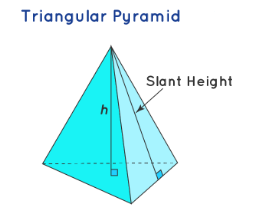
We can calculate the volume of a triangular pyramid with this formula:

\(\color{blue}{Volume\:of\:Triangular\:Pyramid\:=\:\frac{1}{3}\:×\:Base\:Area\:×\:Height}\)

Where we multiply the area of the triangular base by the height of the pyramid (measured from the base to up) and then divide the result by \(3\) according to the formula.

We can calculate the total area of a triangular pyramid by this formula:

\(\color{blue}{Total\:Surface\:area\:of\:a\:Triangular\:Pyramid\:=\:Base\:Area\:+\:\frac{1}{2}\:\left(Perimeter\:of\:the\:base\:×\:Slant\:Height\right)}\)

Geometry for Beginners The Ultimate Step by Step Guide to Acing Geometry

Download

$27.99 Original price was: $27.99.$17.99Current price is: $17.99.

where slant height is the distance from its triangular face along the center of the face to the apex.

Finding the Volume and Surface Area of the Triangular Pyramid,  Example 1:

Find the volume of a triangular pyramid having a base area of \(15\space cm^2\) and a height of \(6\space cm\).

Solution:

Using this formula to find the volume of a triangular pyramid:

\(Volume=\frac{1}{3}×\:Base\:area\:×\:Height\)

\(= \frac{1}{3}× 15 × 6\)

\(=\frac{90}{3}\)

\(= 30\space cm^3\)

Exercises for Finding the Volume and Surface Area of the Triangular Pyramid

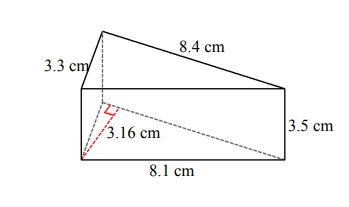
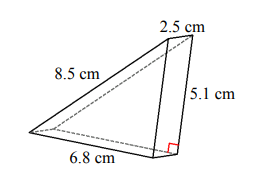
Find the volume and surface area for each triangular pyramid.

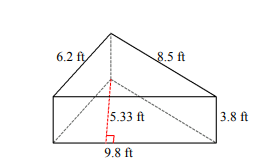
• \(\color{blue}{V= 99.2\space ft^3, A= 145.3\space ft^2}\)
• \(\color{blue}{V= 46.5 \space cm^3, A=95.8\space cm^2}\)
• \(\color{blue}{V=43.4 \space cm^3, A=85.7\space cm^2}\)

Frequently Asked Questions

What is the surface area and volume of a triangular pyramid?

The volume of a triangular pyramid is V = (1/3) × base area × height, and its surface area is the area of the triangular base plus the areas of the three slanted triangular faces. For example, if the base triangle has base 6 and height 4, its area is 12. With a pyramid height of 9, the volume is (1/3) × 12 × 9 = 36 cubic units.

How do you find the volume and surface area of a triangular pyramid?

Start by finding the area of the triangular base with (1/2) × base × height. For volume, multiply that area by the pyramid’s perpendicular height and divide by 3. For surface area, find each of the three side faces with (1/2) × base edge × slant height, then add them to the base area. Keep the two heights separate: the pyramid height goes into volume, and the slant height goes into surface area.

How do you find the volume of a triangular pyramid?

Multiply the base area by the height and take one-third: V = (1/3)Bh. The height must be the straight drop from the apex to the base, not the slant height along a face. Try a right-triangle base with legs 5 and 8: B = (1/2)(5)(8) = 20. If the pyramid is 12 units tall, V = (1/3)(20)(12) = 80 cubic units, one-third of a prism with the same base and height.

What is the volume of a regular triangular pyramid?

A regular triangular pyramid, or regular tetrahedron, has four equilateral faces with the same edge length a, so its volume is V = a³√2/12. For an edge of 6, V = 216√2/12 = 18√2 ≈ 25.46 cubic units. Its surface area is simpler: four equilateral triangles give √3a², which is 36√3 ≈ 62.35 square units for that same edge.

What is the volume and surface area of a pyramid?

For any pyramid, volume is V = (1/3) × base area × height, whatever shape the base is. Surface area is the base area plus the area of every triangular side face. For a regular pyramid this becomes SA = B + (1/2) × perimeter of base × slant height. A triangular pyramid is the case where the base is a triangle, so it has three side faces instead of the four on a square pyramid.

Related Lessons You May Like

• How to find the area of triangles
• How to find volume and surface area of cubes
• How to calculate the volume of cubes and prisms
• Volume of cylinders and spheres
• How to use the Pythagorean Theorem

For a workbook on geometry, Geometry for Beginners walks every topic from first principles. Pre-Algebra for Beginners covers the algebra foundations.