How to Solve Radical Inequalities?

A step-by-step guide to solving radical inequalities

In mathematics, a radical is the opposite of an exponent, denoted by the symbol \(\sqrt{ }\), also known as the root.

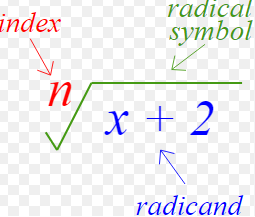
An inequality that has variables inside the radicand is called radical inequality. In other words, a radical inequality is an inequality that has a variable or variables inside the radical symbol.

We can solve radical inequalities using algebra. Some radical inequalities also have variables outside the radical and we can use algebra to calculate them as well. The following steps can be used to solve radical inequalities:

Step 1: Check the index of the radical.

• If the index is even, the final calculated value of the radicand cannot be negative and must be positive. This is called domain restriction.

Step 2: If the index is even, consider the value of the radicand as positive. Solve for the variable x in radicands.

• Therefore, we solve for the variable \(x\) for this radicand when it is greater than or equal to zero. That is, we consider the radicand as \(x\ge 0\) from the radical inequality \(\sqrt[n]{x}<d\) and calculate the variable \(x\).  If the index is odd, however, then consider the radicand as \(x<d\).

Step 3: Solve the original inequality expression algebraically and also remove the radical symbol from the expression.

• We eliminate the radical by taking the index and using it as the exponent in terms of both sides of the inequality. (i.e., \(\sqrt[n]{x}<d\:\rightarrow \:\left(\sqrt[n]{x}\right)^n<d^n)\). Note here that when using the index as an exponent on the radical expression, it nullifies the radical symbol, thus removing it.

Step 4: Test the values to check the solution.

• To test the values of \(x\), we consider a random value that satisfies the inequality. And we will also consider values outside the equality so that we can confirm the correctness of our solution.

Solving Radical Inequalities – Example 1:

solve \(3+\sqrt{4x-4}\le 7\).

Solution:

To solve this radical inequality, first, we check the index of the given radical inequality. Since the index value is not given, the index value is \(2\). Since the index is even, the radicand of the square root will be greater than or equal to zero.

\(4x-4\ge 0\)

\(4x\ge 4\)

\(x\ge 1\)………….. \((1)\)

We now solve the radical inequality algebraically and also remove the radical symbol to simplify it. First, we isolate the radical.

\(3+\sqrt{4x-4}\le 7\rightarrow \sqrt{4x-4}\le 4\)

Now, we remove the radical symbol by taking the index as an exponent on both sides of the inequality.

\(\left(\sqrt{4x-4}\right)^2\le 4^2\)

\(4x-4\le 16\)

\(4x\le 20\)

\(x\le 5\)………….. \((2)\)

Here, we got two inequalities for the value of \(x\) from equations \(1\) and \(2\). So we combine them both and write it as a compound inequality. Then our final answer is:

\(1\le x\le 5\)

Exercises for Solving Radical Inequalities

Solve.

1. \(\color{blue}{\sqrt[3]{x+3}\ge \:2}\)
2. \(\color{blue}{-2\sqrt{x+1}\le -6}\)
3. \(\color{blue}{4\sqrt[3]{x+1}\ge 12}\)

1. \(\color{blue}{x\ge 5}\)
2. \(\color{blue}{\:x\ge 8}\)
3. \(\color{blue}{x\ge 26}\)