How to Solve Piecewise Functions?

The Piecewise function has different definitions depending on the amount of input, i.e., a piecewise function behaves differently for different inputs.

A step-by-step guide to piecewise functions

A piecewise function is a function \(f(x)\) which has different definitions in different intervals of \(x\). The graph of a piecewise function has different parts that correspond to each of its definitions. The absolute value function is a very good example of a piecewise function.  Let us see why is it called so. We know that an absolute value function \(f(x)=| x |\) and is defined as follows: \(\begin{cases}x, \
 if\ x≥0\ \\ -x, \
 if\ x<0\end{cases}\), We need to read this piecewise function as:

• \(f(x)\) is equal to \(x\) when \(x\) is greater than or equal to \(0\) and
• \(f(x)\) is equal to \(-x\) when \(x\) is lesser than \(0\)

Then the diagram \(f(x)\) has two pieces, one corresponding to \(x\) (when \(x\) is in the interval \([0, ∞)\)) and the other corresponding to \(-x\) (when \(x\) is in the interval \((-∞, 0)\)).

Piecewise function graph

The diagram of a piecewise function has several pieces, where each piece corresponds to its definition in an interval. Here are the steps to graph a piecewise function.

• Step 1: First, understand what each definition of a function represents. For example, \(f(x)= ax + b\) represents a linear function (which gives a line), \(f(x)= ax^2+ bx+c\) represents a quadratic function (which gives a parabola), and so on. So that we will have an idea of what shape the piece of the function would result in.
• Step 2: Write the intervals shown in the function definition along with their definitions.
• Step 3: Create a two-column table labeled \(x\) and \(y\) corresponding to each interval. Insert the endpoints of the interval without fail. If the endpoint is removed from the interval, note that we get an open dot corresponding to that point in the graph.
• Step 4: In each table, get more numbers (random numbers) in the \(x\) column that lies in the corresponding interval to get the perfect shape of the graph. If the piece is a straight line, \(2\) values are enough for \(x\). If the piece is not a straight line, take \(3\) or more for \(x\).
• Step 5: Substitute each \(x\) value from each table into the function definition to obtain the corresponding \(y\) values.
• Step 6: Now, just draw all the points from the table (taking care of the open dots) in a graph sheet and connect them by curves.

Domain and range of piecewise function

To find the domain of a piecewise function, we can only look at the definition of the given function. Take the union of all intervals with \(x\) and that will give us the domain.

To find the range of a piecewise function, the easiest way is to plot it and look at the \(y\)-axis. See what \(y\)-values are covered by the graph.

Evaluating piecewise function

To evaluate a piecewise function at any given input,

• First, see which of the given intervals (or inequalities) the given input belongs.
• Then just replace the given input in the function definition corresponding to that particular interval.

Piecewise continuous function

A piecewise continuous function, as its name implies, is a continuous function, which means, its graph has different pieces in it but still we will be able to draw the graph without lifting the pencil.

Exercises for Piecewise Functions

Graph the piecewise function.

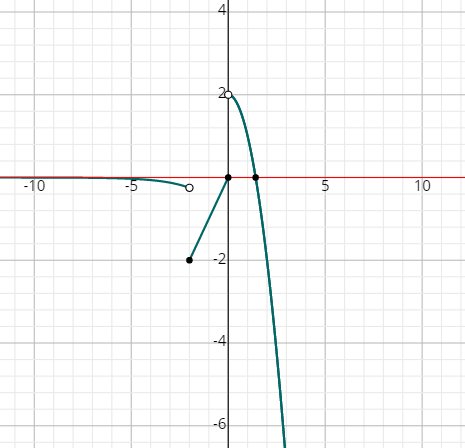
• \(\color{blue}{\begin{cases}-2^x, x<−2 \\ −|x|, −2≤x≤0\\2-x^2, x>0\end{cases}}\)

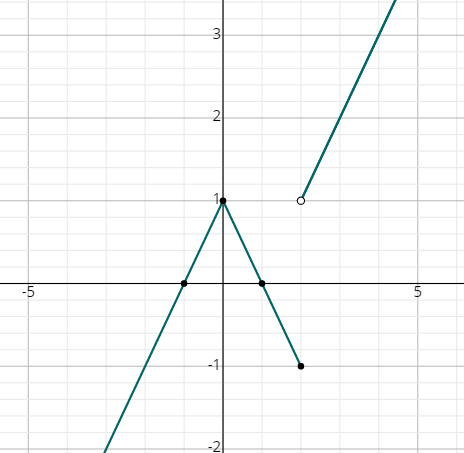
• \(\color{blue}{\begin{cases}x+1, x<0 \\ −x+1, 0≤x≤2\\x-1, x>2\end{cases}}\)

• \(\color{blue}{\begin{cases}-2^x, x<−2 \\ −|x|, −2≤x≤0\\ 2-x^2, x>0\end{cases}}\)

• \(\color{blue}{\begin{cases}x+1, x<0 \\ −x+1, 0≤x≤2\\x-1, x>2\end{cases}}\)