How to Solve Double Angle Identities?
A double angle formula is a trigonometric identity that expresses the trigonometric function \(2θ\) in terms of trigonometric functions \(θ\). In this step-by-step guide, you will learn more about double-angle formulas.
[include_netrun_products_block from-products="product/6-south-carolina-sc-ready-grade-3-math-practice-tests/" product-list-class="bundle-products float-left" product-item-class="float-left" product-item-image-container-class="p-0 float-left" product-item-image-container-size="col-2" product-item-image-container-custom-style="" product-item-container-size="" product-item-add-to-cart-class="btn-accent btn-purchase-ajax" product-item-button-custom-url="{url}/?ajax-add-to-cart={id}" product-item-button-custom-url-if-not-salable="{productUrl} product-item-container-class="" product-item-element-order="image,title,purchase,price" product-item-title-size="" product-item-title-wrapper-size="col-10" product-item-title-tag="h3" product-item-title-class="mt-0" product-item-title-wrapper-class="float-left pr-0" product-item-price-size="" product-item-purchase-size="" product-item-purchase-wrapper-size="" product-item-price-wrapper-class="pr-0 float-left" product-item-price-wrapper-size="col-10" product-item-read-more-text="" product-item-add-to-cart-text="" product-item-add-to-cart-custom-attribute="title='Purchase this book with single click'" product-item-thumbnail-size="290-380" show-details="false" show-excerpt="false" paginate="false" lazy-load="true"]
The double angle formulas are used to find the values of double angles of trigonometric functions using their single angle values. Also, the double-angle formulas can be used to derive the triple-angle formulas.
Related Topics
A step-by-step guide to double angle formulas
The double angle formulas are the special cases of the sum formulas of trigonometry and some alternative formulas are derived by using the Pythagorean identities. The sum formulas of trigonometry are:
- \(\color{blue}{sin\:\left(A\:+B\right)=sin\:A\:cos\:B\:+\:cos\:A\:sin\:B}\)
- \(\color{blue}{cos\:\left(A\:+\:B\right)=\:cos\:A\:cos\:B\:-\:sin\:A\:sin\:B}\)
- \(\color{blue}{tan\:\left(A\:+\:B\right)=\:\frac{\left(tan\:A\:+\:tan\:B\right)}{\left(1\:-\:tan\:A\:tan\:B\right)}}\)
What are double-angle formulas?
We derive double-angle formulas of \(sin, cos,\) and \(tan\) by substituting \(A=B\) in each of the above-sum formulas. Also, we will extract some alternative formulas that are derived using Pythagorean identities.
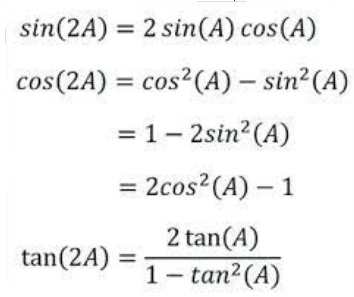
Double Angle Formulas – Example 1:
If \(tan A= \frac{3}{5}\), find the values of \(sin\:2A\).
Solution:
Since the value of \(tan\:A\) is given, we use the double angle formulas for finding \(sin\:2A\).
\(sin\:2A=\frac{2\:tan\:A}{1+tan^2A}\)
\(=\frac{2\left(\frac{3}{5}\right)^2}{1+\left(\frac{3}{5}\right)^2}\)
\(=\frac{\frac{18}{25}}{\frac{34}{25}}\)
\(=\frac{18\times 25}{25\times 34}\)
\(=\frac{9}{17}\)
Exercises for Double Angle Formulas
- Find a formula for \(cos(4x)\) in terms of \(cos x\).
- Solve the equation \(sin\:2x\:=\:cos\:x,\:0\:\le \:x\:<\pi\).
- \(\color{blue}{8\:cos^4x-8\:cos^2x+1}\)
- \(\color{blue}{x=\frac{\pi }{2},\frac{\pi }{6},\frac{5\pi }{6}}\)
Related to This Article
More math articles
- 8th Grade Wisconsin Forward Math Worksheets: FREE & Printable
- 8th Grade NHSAS Math Worksheets: FREE & Printable
- Full-Length CLEP College Mathematics Practice Test-Answers and Explanations
- Full-Length 7th Grade PARCC Math Practice Test-Answers and Explanations
- How to Solve Pythagorean Theorem Problems? (+FREE Worksheet!)
- Top 10 Tips to ACE the ISEE Math Test
- Converting Units of Weight/Mass for 4th Grade
- Algebra Puzzle – Challenge 47
- How to Manage Your Time Effectively on the ISEE Math Test?
- 3rd Grade NSCAS Math Worksheets: FREE & Printable
What people say about "How to Solve Double Angle Identities? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.