How to Graph the Cotangent Function?
Cotangent is one of the trigonometric ratios. In this step-by-step guide, you will learn more about the graph of the cotangent function.

Step-by-step guide to graphing the cotangent function
Cotangent is one of the basic trigonometric ratios. It is usually represented as \(cot x\), where \(x\) is the angle between the base and the hypotenuse of a right triangle. Alternative names of cotangent are cotan and cotangent \(x\).
The cotangent formula is:
\(\color{blue}{cot\:θ=\frac{Adjacent\:side}{Opposite\:side}}\)
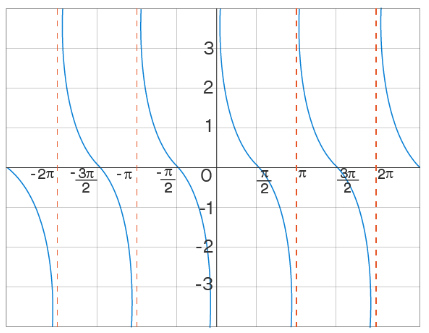
Since the cotangent function is not defined for integer multiples of \(π\), the vertical asymptote exists at all multiples of \(π\) in the cotangent graph. Also, the cotangent is \(0\) at all odd multiples of \(\frac{π}{2}\). Also, in an interval say \((0, π)\), the values of the cot decrease as the angles increase. So \(cot\) is a decreasing function. Then, the graph of the cotangent function looks like this.
Related to This Article
More math articles
- Decimals in Action: Completing Addition and Subtraction Sentences
- 8th Grade Scantron Math Worksheets: FREE & Printable
- Best Digital Writing Pads for Online Teaching in 2024
- 10 Most Common 6th Grade STAAR Math Questions
- How to Graph Translations on the Coordinate Plane?
- Full-Length 8th Grade ACT Aspire Math Practice Test
- FREE 7th Grade New York State Testing Program Math Practice Test
- How to Use Exponents to Write Powers of Ten?
- How to Graph an Equation in the Standard Form?
- Derivatives Demystified: Everything You Need to Know



















What people say about "How to Graph the Cotangent Function? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.