Full-Length ISEE Middle Level Math Practice Test-Answers and Explanations

Did you take the ISEE Middle-Level Math Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.

ISEE Middle Level Math Practice Test Answers and Explanations

ISEE Middle Level Practice Test
Quantitative Reasoning

1- Choice D is correct
\(15\%\) off equals \($18\). Let x be the original price of the table. Then:
\(15\%\) of \(x=18→0.15x=18→x=\frac{18}{0.15}=120\)

2- Choice B is correct
\(981,364,454×\frac{1}{10,000,000}=98.1364454\)

3- Choice C is correct
\(\frac{1}{8}≅0.125, \frac{1}{3}≅0.33, \frac{1}{2}=0.5, \frac{3}{5}=0.6\)

4- Choice C is correct
Method 1: \(5×5×5×5=625\), Method 2: \(8^x=512\)
Let’s review the choices provided:
A. \(2\) →\(5^x=625→5^2=25\)
B. \(3\) →\(5^x=625→5^3=125\)
C. \(4\) →\(5^x=625→5^4=625\)
D. \(5\) →\(5^x=625→5^5=3125\)
Choice C is correct.

5- Choice C is correct
\(2g=2×(-2x-2y)=-4x-4y\)
\( f-2g=4x-y-(-4x-4y)=8x+3y\)

6- Choice A is correct
\(\frac{-45 × 0.8}{4}=-\frac{45×\frac{8}{10}}{4}=-\frac{\frac{360}{10}}{4}=-\frac{360}{40}=-9\)

7- Choice A is correct
Use the formula for Percent of Change: \(\frac{New \space Value\space-\space Old \space Value}{Old \space Value}× 100 \%\)
\(\frac{43.2-54}{54}× 100\% = –20\%\) (negative sign here means that the new price is less than old price)

8- Choice A is correct
Supplementary angles sum up to 180 degrees. x and 33 degrees are supplementary angles. Then: \(x=180^\circ -33^\circ=147^\circ\)

9- Choice C is correct
Use the formula of areas of circles.
Area of a circe \(= πr^2 ⇒ 36 π = r^2 ⇒ 36 = r^2 ⇒ r = 6\)
Radius of the circle is 6. Now, use the circumference formula:
Circumference \(= 2πr = 2π(6) = 12π\)

10- Choice D is correct
\(2.21=\frac{221}{100} \) and \(6.5=\frac{65}{10} →2.21×6.5=\frac{221}{100}×\frac{65}{10}=\frac{14365}{1000}=14.365≅14.4\)

11- Choice C is correct
If the score of Mia was 80, therefore the score of Ava is 40. Since the score of Emma was half as that of Ava, therefore, the score of Emma is 20.

12- Choice A is correct
The perimeter of the trapezoid is 60.
Therefore, the missing side (height) is \(= 60 – 10 – 20 – 12 = 18\)
Area of the trapezoid: A \(= \frac{1}{2} h (b_1 + b_2) = \frac{1}{2}(18) (10 + 12) = 198\)

13- Choice C is correct
Add the first 4 numbers. \(50 + 48 + 42 + 52 = 192\)
To find the distance traveled in the next 4 hours, multiply the average by number of hours.
Distance = Average \(×\) Rate\( = 50 × 4 = 200\), Add both numbers.\( 200 + 192 = 392\)

14- Choice D is correct
Mean\(=\frac{12+22+34+46+52+68+72+86}{8}=\frac{392}{8}=49\)

15- Choice D is correct
Let \(x\) be the number. Write the equation and solve for \(x\).
\(\frac{2}{3}×36=\frac{4}{9}\). \(x ⇒ \frac{2×36}{3}= \frac{4x}{9}\), use cross multiplication to solve for \(x\).
\(9×72=4x×3 ⇒648=12x ⇒ x=54\)

16-Choice B is correct
Simplify: \(-2(2x+3)=3(4-2x), -4x-6=12-6x\), Add \(4x\) from both sides: \(-6=-2x+12\), subtract 12 to both sides: \(-18 = -2x, 9 = x\)

17–Choice B is correct
\(\frac{3}{4}\) of \(240=\frac{3}{4}×240=180\), \(\frac{1}{3}\) of \(180=\frac{1}{3}×180=60\)

18–Choice C is correct
The ratio of boys to girls is 6:8. Therefore, there are 6 boys out of 14 students. To find the answer, first, divide the total number of students by 14, then multiply the result by 6.
\( 70 ÷ 14 = 5 ⇒ 5× 6 = 30\)
There are 30 boys and 40 (\(70 – 30\)) girls. So, 10 more boys should be enrolled to make the ratio 1:1

19–Choice D is correct
Let \(x\) be the original price. If the price of a laptop is decreased by \(20\%\) to $420, then: \(0.8\%\) of \(x=420⇒ 0.8x=420 ⇒ x=420÷0.8=525\)

20-Choice C is correct
Let \(x\) be the sales profit. Then, \(2\%\) of sales profit is \(0.03x\). Employee’s revenue: \(0.03x+6,500\)

21-Choice C is correct
Petrol of car A in 300km=\(\frac{7×300}{100}=21\), Petrol of car B in 300km = \(\frac{9×300}{100}=27, 27-21=6\)

22-Choice B is correct
\(x=105+35=140\)

23-Choice D is correct
The diagonal of the square is 10. Let \(x\) be the side.
Use Pythagorean Theorem:\(a^2 + b^2 = c^2\)
\(x^2 + x^2 = 102 ⇒ 2x^2 = 102 ⇒ 2x^2 = 100 ⇒x^2 = 50 ⇒x= \sqrt{50}\)

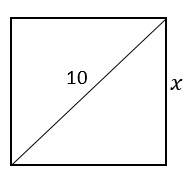
The area of the square is:
\(\sqrt{50} × \sqrt{50} = 50\)

24-Choice A is correct
\(-42-(-73)=-42+73=73-42=31\)

25-Choice D is correct
Choice B is correct Simplify: \(-2(2x+3)=3(4-2x), -4x-6=12-6x\), Add \(4x\) from both sides: \(-6=-2x+12\), subtract 12 to both sides: \(-18 = -2x, 9 = x\)
Let’s review the choices:
A. \(4/5>0.8\) This is not a correct statement. Because \(\frac{4}{5}=0.8\) and it’s less than 0.8.
B. \(12\%=\frac{1}{5}\) This is not a correct statement. Because \(12\% = 0.12\) and \(\frac{1}{5}=0.2\)
C. \(4<\frac{6}{2}\) This is not a correct statement. Because \(\frac{6}{2}=3\) and it’s less than 4.
D. \(\frac{8}{9}>0.8\) This is a correct statement.
\(\frac{8}{9}=0.88→0.8<\frac{8}{9}\)

The Absolute Best Book to Ace the ISEE Middle Level Math Test

26-Choice A is correct
Column A: Use the order of operation to calculate the result. \(5+5×7-4=5+35-4=36\)
Column B: \(4+6×6-6→4+36-6=34\)

27-Choice A is correct
Column A: The value of \(x\) when \(y=9\) : \(y=3x+18→9=3x+18→3x=-9→x=-3\)
Column B: \(-4\), \(-3\) is greater than \(-4\).

28-Choice C is correct
Column A: Simplify. \(\sqrt{25}+\sqrt{25}=5+5=10, 10\) is equal to \(\sqrt{100}(\sqrt{100}=10)\)

29-Choice D is correct
Column A: Based on the information provided, we cannot find the average age of Joe and Michelle or the average age of Michelle and Nicole.

30-Choice A is correct
Column A: Simplify. \(\sqrt{144-12}=\sqrt{23}\)
Column B: \(\sqrt{144}-\sqrt{121}=12-11=1\) , \(\sqrt{23}\) is bigger than 1.

31-Choice A is correct
The volume of a right cylinder \(= πr^2 h→80π=πr^2 h=π(5)^2 h→h=3.2\)
The height of the cylinder is 3.2 inches which are bigger than 3 inches.

32-Choice D is correct
Choose different values for x and find the value of quantity A.
\(x=1\), then: Quantity A: \(\frac{2}{X}+x= \frac{2}{1}+1=3\), Quantity B is greater
\(x=0.1\), then: Quantity A: \(\frac{2}{X}+x= \frac{2}{0.1}+1=20+1=21\), Quantity A is greater The relationship cannot be determined from the information given.

33-Choice B is correct
Simply change the fractions to decimals. \(\frac{2}{5}=0.40, \frac{5}{9}=0.55…, \frac{5}{8}=0.625,\) Quantity B is greater

34-Choice A is correct
Simplify quantity B. Quantity B: \((\frac{x}{3})^3=\frac{x^3}{3^3 }\)
Since the two quantities have the same numerator (\(x^3\)) and the denominator in quantity B is bigger \((3^3>3)\), then the quantity A is greater.

35-Choice A is correct
Quantity A is: \(\frac{5+6+x}{3}=6→x=7\), Quantity B is: \(\frac{(7+(7+3)+(7+1)-7)}{4}=4.5\)

36-Choice C is correct
Choose different values for a and b and find the values of quantity A and quantity B.
\(a=4\) and \(b=3\), then: Quantity A: \(|4 – 3|=|1|=1\), Quantity B: \(|3 – 4|=|1|=1\)
The two quantities are equal. a=3 and b=-3, then: Quantity A: \(|3+3|=|6|=6\)
Quantity B: \(|- 3 – (3)|=|-6|=6\), The two quantities are equal.
Any other values of a and b provide the same answer.

37-Choice C is correct
\(4x^3-80=176→4x^3=176+80=256→x^3=\frac{256}{4}=64→x=\sqrt[3]{64}=\sqrt[3]{4^3}=4\)
\(3-4y=-13→-4y=-13-3=-16→y=\frac{-16}{-4}=4\)

38-Choice B is correct
Number of pencils are blue\(=75-33=42\), Percent of blue pencils is: \(\frac{42}{75}×100=56\%\)

39-Choice A is correct
\(\frac{4}{6}×120=80\)

40-Choice C is correct
\(2(\frac{3}{5}-\frac{6}{10})+2=2×(\frac{6-6}{10})+2=0+2=2\)

41-Choice B is correct
\(12\%\) of \(160=\frac{12}{100}×160=19.2\), Let \(x\) be the number then, \(x=19.2+15=34.2\)

42-Choice C is correct
Let \(x\) be the number. Write the equation and solve for \(x\). \((21 – 2x) ÷ x = 5\)
Multiply both sides by \(x\). \((21 – 2x) = 5x\), then add x both sides. \(21 = 7x\), now divide both sides by 7. \(x = 3\)

43-Choice A is correct
\(25\%\) of \(48\) is: \(\frac{25}{100}×48=\frac{1200}{100}=12\), Let \(x\) be the number then: \(x=12-3=9\)

44-Choice A is correct
The perimeter of rectangle is: \(2×(6+5)=2×11=22\)
The perimeter of circle is: \(2πr=2×3×\frac{12}{2}=36\), Difference in perimeter is: \(36-22=14\)

45-Choice A is correct
Use this formula: Percent of Change = \(\frac{New \space Value-Old \space Value}{Old \space Valu}× 100 \%\)
\(\frac{21000-25000}{25000} × 100 \% = 16 \% \space and \space \frac{17640-21000}{21000} × 100 \% = 16 \%\)

46-Choice D is correct
\((2x-3)^3=125→2x-3=\sqrt[3]{125}=\sqrt[3]{5^3} =5→2x=5+3→x=\frac{8}{2}=4\)

47-Choice B is correct
\((\frac{10}{4}×24)+(\frac{5}{2}×10)=(60)+(25)=85\)

48-Choice D is correct
If \(\frac{x}{2}=24\), then \(x=48\), \(\frac{5x}{8}=\frac{5×48}{8}=\frac{240}{8}=30\)

49-Choice C is correct
\(\frac{3}{4}=0.75, \frac{7}{9}=0.77, 85%=0.85\)

50-Choice B is correct
Area\(=πr^2=π×(\frac{22}{2})^2=121π=121×3.14≅379.94=380\)

51-Choice A is correct
First, find the number. Let \(x\) be the number. Write the equation and solve for \(x\).
\(160 \%\) of a number is \(128\), then: \(1.6×x=128 ⇒ x=128÷1.6=80\),
\(60 \% \space \)of\( \space 80 \space is: 0.6 × 80 = 48\)

52-Choice D is correct
\(\frac{3}{5}×45=\frac{135}{5}=27\)

53-Choice A is correct
All angles in a triangle sum up to 180 degrees. Then:
\(2α+90^\circ=180^\circ→2α=90→α=45^\circ\)

54-Choice B is correct
The sum of angles in the rectangle is 360.

55-Choice B is correct
Find the difference of each pairs of numbers: 5,8,13,21,34,_,89
The sum of \(5,8\) is \(13\). The sum of \(8,13\) is \(21\). The sum of \(13,21\) is \(34\). The sum of \(34\) and x is \(89\).Thus \(x=89-34=55\)

56-Choice D is correct
\(\frac{4}{6}×96=\frac{384}{6}=64\)

57-Choice D is correct
The capacity of a red box is \(25\%\) greater than a blue box. Let \(x\) be the capacity of the blue box. Then: \(x+25\% \space of \space x=40→1.25x=40→x=\frac{40}{1.25}=32\)

58-Choice C is correct
The question is this: 1.65 is what percent of 1.2?
Use percent formula: Part = \(\frac{percent}{100}× whole, 1.65= \frac{percent}{100}× 1.2 ⇒ 1.65 = \frac{percent ×1.2}{100} ⇒165 = percent ×1.2 ⇒ percent = \frac{165}{1.2} =137.5\)

59-Choice A is correct
60 minutes = 1Hours→\(\frac{315}{60}=5.25\) Hours

60-Choice A is correct
Let \(x\) be the number of shoes the team can purchase. Therefore, the team can purchase \(120 x\).
The team had \($32,000\) and spent \($20,000\). Now the team can spend on new shoe \($12000\) at most. Now, write the inequality: \(140x+20,000≤32,000\)

Best ISEE Middle Level Math Prep Resource for 2022

61-Choice D is correct
78 is not a prime number, it is divisible by 3 and13.

62-Choice A is correct
The width of a rectangle is \(5x\) and its length is \(7x\). Therefore, the perimeter of the rectangle is 24x. Perimeter of a rectangle=2(width+length)\(=2(5x+7x)=2(12x)=24x\)
The perimeter of the rectangle is 108. Then: \(24x=108→x=4.5\)

63-Choice D is correct
$18 is what percent of $63? \(18 ÷ 60 = 0.3 = 30\%\)

64-Choice B is correct
Let x be one-kilogram orange cost, then: \(2x+(5×5.2)=34→2x+26=34→x=34-26→2x=8→x=\frac{8}{2}=$4\)

65-Choice D is correct
\((((-18)+44)×(-4))+80=(26×(-4)+80=(-104)+80=24\)

66-Choice C is correct
The area of the square is 81 inches. Therefore, the side of the square is the square root of the area. \(\sqrt{81}=9\) inches, Four times the side of the square is the perimeter: \(4 × 9 = 36\) inches

67-Choice C is correct
The distance between Jason and Joe is 12 miles. Jason running at 6.4 miles per hour and Joe is running at the speed of 8 miles per hour. Therefore, every hour the distance is 1.6 miles less. \(12 ÷ 1.6 = 7.5\)

68-Choice A is correct
The ratio of lions to tigers is 6 to 4 at the zoo. Therefore, the total number of lions and tigers must be divisible by 10. \(6+4=10\), From the numbers provided, only 64 is not divisible by 10.

69-Choice B is correct
The percent of girls playing tennis is: \(30 \% × 50 \% = 0.3 × 0.5 = 0.15 = 15 \%\)

70-Choice A is correct
There are triple as many girls as boys. Let x be the number of girls in the class. Then:
\(x+3x=56→4x=56→x=14\)

71-Choice D is correct
Use PEMDAS (order of operation):
\([(-3)×(-12)+4]-(-2)+[3×6]÷6=[36+4]-(-2)+18÷6=40+2+3=45\)

72-Choice C is correct
\(1024=4^x →4^x=4^5→x=5\)

73-Choice A is correct
Number of rotates in 15 second\(=\frac{360×15}{12}=450\)

74-Choice C is correct
\(6x+8=2x-12→4x+8=-12→4x=-20→x=\frac{-20}{4}=-5\)

75-Choice B is correct
Use formula of rectangle prism volume.
V = (length) (width) (height) ⇒ 1260 = (18) (14) (height) ⇒ height = \(1260 ÷ 252 = 5\)

76-Choice B is correct
Let x be the original price. If the price of the sofa is decreased by \(20\%\) to $380, then: \(80 \% \space\) of\( \space x=380 ⇒ 0.80 x=380 ⇒ x=380÷0.80=475\)

77-Choice A is correct
The area of trapezoid is: \((\frac{(10+12)}{2})×8=88\)

78-Choice D is correct
Write the equation and solve for B:
\(0.20A=0.40B \), divide both sides by \(0.40\), then you will have \(\frac{0.20}{0.40} A=B\) , therefore: \(B=\frac{1}{2} A\), and B is \(0.5\) times of A or it’s \(50\%\) of A.

79-Choice B is correct
\(2x-(12-x)=x+20→2x-12+x=x+20→2x=32→x=16\)

80-Choice B is correct
15-11.56=$3.44

81-Choice D is correct
\(12.56÷0.08=\frac{\frac{1256}{100}}{\frac{8}{100}}=\frac{1256}{8}=157\)

82-Choice B is correct
The probability of choosing a Hearts or 10 is(one of 10 is heart) \(\frac{13+(4-1)}{52}=\frac{16}{52}=\frac{4}{13}\)

83–Choice C is correct
\(\frac{1}{3}+\frac{\frac{8}{10}}{\frac{6}{12}}=\frac{1}{3}+\frac{812}{106}=\frac{1}{3}+\frac{96}{60}=\frac{20+96}{60}=\frac{116}{60}=1\frac{56}{60}=1\frac{14}{15}\)

84-Choice A is correct
\(\frac{8×14}{90}=\frac{112}{90}=1.24≅1.2\)

The Best Books to Ace the ISEE Middle Level Math Test