Dividing Mixed Numbers for 5th Grade: Step-by-Step Guide

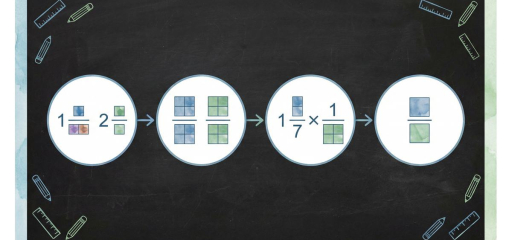
Dividing mixed numbers is used when splitting quantities into equal parts of a given size—for example, “a ribbon is \(4 \frac{1}{2}\) feet and is cut into pieces of \(1 \frac{1}{2}\) feet each—how many pieces?” In Grade 5, students divide mixed numbers by first converting them to improper fractions, then applying the “multiply by the reciprocal” rule for fraction division.

The process: Convert each mixed number to an improper fraction, then divide as with fractions—multiply the first fraction by the reciprocal of the second. Simplify and convert the result back to a mixed number if needed. For example, \(2 \frac{1}{2} \div 1 \frac{1}{4} = \frac{5}{2} \div \frac{5}{4} = \frac{5}{2} \times \frac{4}{5} = \frac{20}{10} = 2\).

DETAILED EXPLANATION

Steps to divide mixed numbers:

1. Convert each mixed number to an improper fraction.

The Absolute Best Book to Ace Grade 5 Math

The Ultimate Elementary School Math Bundle Grade 3-5

Download

$109.99 Original price was: $109.99.$54.99Current price is: $54.99.

2. Change division to multiplication and use the reciprocal of the divisor.

3. Multiply the fractions.

4. Simplify and convert to a mixed number if needed.

Conversion: \(a \frac{b}{c} = \frac{a \times c + b}{c}\).

Example: \(3 \frac{1}{3} \div 2 \frac{1}{2} = \frac{10}{3} \div \frac{5}{2} = \frac{10}{3} \times \frac{2}{5} = \frac{20}{15} = \frac{4}{3} = 1 \frac{1}{3}\).

WORKED EXAMPLES WITH STEP BY STEP SOLUTIONS

Example 1

Divide \(2 \frac{1}{2} \div 1 \frac{1}{4}\)

The Ultimate Middle School Math Bundle: Grades 6–8

Solutions:

Step 1: Convert to improper fractions: \(2 \frac{1}{2} = \frac{5}{2}\); \(1 \frac{1}{4} = \frac{5}{4}\).

Step 2: Change to multiplication with reciprocal: \(\frac{5}{2} \div \frac{5}{4} = \frac{5}{2} \times \frac{4}{5}\).

Step 3: Multiply: \(\frac{5 \times 4}{2 \times 5} = \frac{20}{10} = 2\).

Step 4: The quotient is 2.

Answer: 2

Example 2

\(3 \frac{1}{3} \div 2 \frac{1}{2}\) = ?

Solutions:

Mastering Grade 5 Math

Mastering Grade 5 Math The Ultimate Step by Step Guide to Acing 5th Grade Math

Download

$29.99 Original price was: $29.99.$16.99Current price is: $16.99.

Step 1: Convert: \(3 \frac{1}{3} = \frac{10}{3}\); \(2 \frac{1}{2} = \frac{5}{2}\).

Step 2: \(\frac{10}{3} \div \frac{5}{2} = \frac{10}{3} \times \frac{2}{5}\).

Step 3: Multiply: \(\frac{20}{15}\). Simplify: \(\frac{20}{15} = \frac{4}{3}\).

Step 4: Convert: \(\frac{4}{3} = 1 \frac{1}{3}\).

Answer: \(1 \frac{1}{3}\)

Example 3

A ribbon is \(4 \frac{1}{2}\) feet. It is cut into pieces of \(1 \frac{1}{2}\) feet each. How many pieces?

Solutions:

Step 1: Divide total length by piece length: \(4 \frac{1}{2} \div 1 \frac{1}{2}\).

Step 2: Convert: \(4 \frac{1}{2} = \frac{9}{2}\); \(1 \frac{1}{2} = \frac{3}{2}\).

Step 3: \(\frac{9}{2} \div \frac{3}{2} = \frac{9}{2} \times \frac{2}{3} = \frac{18}{6} = 3\).

Step 4: There are 3 pieces.

Answer: 3 pieces

Example 4

Divide \(1 \frac{3}{4} \div \frac{1}{2}\)

Solutions:

Step 1: Convert mixed: \(1 \frac{3}{4} = \frac{7}{4}\). The divisor \(\frac{1}{2}\) is already a fraction.

Step 2: \(\frac{7}{4} \div \frac{1}{2} = \frac{7}{4} \times \frac{2}{1} = \frac{14}{4} = \frac{7}{2}\).

Step 3: Convert: \(\frac{7}{2} = 3 \frac{1}{2}\).

Answer: \(3 \frac{1}{2}\)