Converting Decimals to Fractions for 5th Grade: Place Value

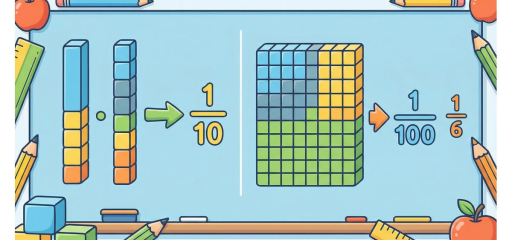
Converting decimals to fractions helps us work with measurements, simplify comparisons, and understand decimals as parts of a whole. In Grade 5, students convert decimals to fractions using place value: the last decimal place tells us the denominator (tenths → 10, hundredths → 100, thousandths → 1000), and the digits form the numerator. We then simplify the fraction to lowest terms.

For example, 0.5 = 5 tenths = \(\frac{5}{10} = \frac{1}{2}\). And 0.34 = 34 hundredths = \(\frac{34}{100} = \frac{17}{50}\). The key is to identify the place value of the last digit, write the decimal as a fraction with that place value as the denominator, and simplify.

DETAILED EXPLANATION

Steps to convert a decimal to a fraction:

1. Identify the place value of the last digit (rightmost nonzero digit, or the last digit if there are zeros).

The Absolute Best Book to Ace Grade 5 Math

The Ultimate Elementary School Math Bundle Grade 3-5

Download

$109.99 Original price was: $109.99.$54.99Current price is: $54.99.

2. Write the decimal as a fraction: the digits (ignoring the decimal point) form the numerator; the denominator is the place value (10, 100, 1000, etc.).

3. Simplify the fraction by dividing numerator and denominator by their GCF.

Example: 0.5 → 5 tenths → \(\frac{5}{10} = \frac{1}{2}\).

Example: 0.34 → 34 hundredths → \(\frac{34}{100} = \frac{17}{50}\).

Example: 0.125 → 125 thousandths → \(\frac{125}{1000} = \frac{1}{8}\).

WORKED EXAMPLES WITH STEP BY STEP SOLUTIONS

Example 1

Convert 0.5 to a fraction.

The Ultimate Middle School Math Bundle: Grades 6–8

The Ultimate Middle School Math Bundle Grades 6-8

Download

$109.99 Original price was: $109.99.$54.99Current price is: $54.99.

Solutions:

Step 1: 0.5 has one decimal place. The 5 is in the tenths place.

Step 2: 0.5 = 5 tenths = \(\frac{5}{10}\).

Step 3: Simplify: GCF(5, 10) = 5. \(\frac{5}{10} = \frac{1}{2}\).

Answer: \(\frac{1}{2}\)

Example 2

Convert 0.34 to a fraction.

Solutions:

Step 1: 0.34 has two decimal places. The 4 is in the hundredths place, so we use hundredths.

Mastering Grade 5 Math

Mastering Grade 5 Math The Ultimate Step by Step Guide to Acing 5th Grade Math

Download

$29.99 Original price was: $29.99.$16.99Current price is: $16.99.

Step 2: 0.34 = 34 hundredths = \(\frac{34}{100}\).

Step 3: Simplify: GCF(34, 100) = 2. \(\frac{34}{100} = \frac{17}{50}\).

Answer: \(\frac{17}{50}\)

Example 3

Jake ran 0.75 mile. Write this as a fraction.

Solutions:

Step 1: 0.75 = 75 hundredths = \(\frac{75}{100}\).

Step 2: Simplify: GCF(75, 100) = 25. \(\frac{75}{100} = \frac{3}{4}\).

Step 3: Jake ran \(\frac{3}{4}\) mile.

Answer: \(\frac{3}{4}\) mile

Example 4

Convert 0.125 to a fraction.

Solutions:

Step 1: 0.125 = 125 thousandths = \(\frac{125}{1000}\).

Step 2: Simplify: GCF(125, 1000) = 125. \(\frac{125}{1000} = \frac{1}{8}\).

Answer: \(\frac{1}{8}\)