10 Most Common 4th Grade FSA Math Questions
Want to help your 4th-grade student prepare for the FSA Math test? Want a preview of the most common mathematics questions on the 4th Grade FSA Math test? If so, then you are in the right place.
The mathematics section of 4th Grade FSA can be a challenging area for many test-takers, but with enough patience, it can be easy and even enjoyable!
Preparing students for the 4th Grade FSA Math test can be a nerve-wracking experience. Learning more about what they’re going to see when they take the 4th Grade FSA can help to reduce those pre-test jitters. Here’s a chance to review the 10 most common 4th Grade FSA Math questions to help your students know what to expect and what to practice most. Let your students try these 10 most common 4th Grade FSA Math questions to hone their mathematical skills and to see if their math skills are up to date on what’s being asked on the exam or if they still need more practice.
Make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions students need to practice for the 4th Grade FSA Math test.
The Absolute Best Book to Ace 4th Grade FSA Math Test
10 Sample 4th Grade FSA Math Practice Questions
1- Use the picture below to answer the question.
Which decimal number names the shaded part of this square?
A. \(0.08\)
B. \(0.20\)
C. \(0.92\)
D. \(0.98\)
2- Which number correctly completes the number sentence \(80 × 34 =\)?
A. \(272\)
B. \(560\)
C. \(1920\)
D. \(2720\)
3- Use the table below to answer the question.
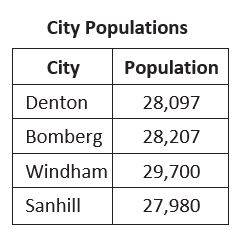
Which list of city populations is in order from least to greatest?
A. \(28,097; 28,207; 29,700; 27,980\)
B. \(29,700; 28,207; 28,097; 27,980\)
C. \(27,980; 28,097; 28,207; 29,700\)
D. \(27,980; 28,207; 28,097; 29,700\)
4- Which number correctly completes the subtraction sentence
\(5.0 – 3.25 =\) _______ ?
A. \(1.25\)
B. \(1.75\)
C. \(2.25\)
D. \(2.75\)
5- For a concert, there are children’s tickets and adult tickets for sale. Of the total available tickets, \(\frac{26}{100}\) have been sold as adult tickets and \(\frac{4}{10}\) as children’s tickets. The rest of the tickets have not been sold.
What fraction of the total number of tickets for the concert have been sold?
A. \(\frac{30}{100}\)
B. \(\frac{66}{100}\)
C. \(\frac{30}{10}\)
D. \(\frac{66}{110}\)
6- Mia has a group of shapes. Each shape in her group has at least one set of parallel sides. Each shape also has at least one set of perpendicular sides. Which group could be Mia’s group of shapes?
A.
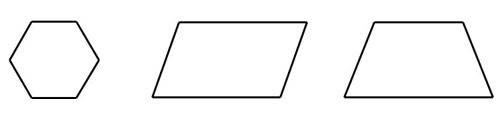
B.
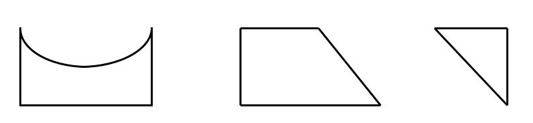
C.
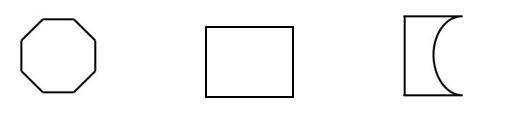
D.
7- There are \(86\) students from Riddle Elementary school at the library on Monday. The other \(32\) students in the school are practicing in the classroom. Which number sentence shows the total number of students in Riddle Elementary school?
A. \(86 + 32\)
B. \(86 -32\)
C. \(86 × 32\)
D. \(86 ÷ 32\)
8- Carol is inviting \(5\) friends to a party. She has \(40\) cookies. How many cookies will each friend get? _________
9- Moe packs \(55\) boxes with flashcards. Each box holds \(100\) flashcards. How many flashcards Moe can pack into these boxes?
A. \(5505\)
B. \(550\)
C. \(275\)
D. \(5500\)
10- A stack of \(7\) pennies has a height of 1 centimeter. Nick has a stack of pennies with a height of \(4\) centimeters. Which equation can be used to find the number of pennies, \(n\), in Nick’s stack of pennies?
A.\(n = 7 + 4\)
B. \(n = 7- 4\)
C. \(n = 7×4\)
D. \(n = 7 ÷ 4\)
Best 4th Grade FSA Math Exercise Resource for 2022
Answers:
1- C
The model is divided into \(100\) equal parts. We shade 92 parts that it’s equal to \(\frac{92}{100}\) or \(0.92\).
2- D
\(80 × 34 =2720\)
3- C
\(27,980 ≤ 28,097 ≤ 28,207 ≤ 29,700\)
4- B
\(5.0 – 3.25 =1.75\)
5- B
Add adult tickets and children’s ticket that have been sold.
\(\frac{26}{100}+\frac{4}{10}=\frac{26 + 40}{100}=\frac{66}{100}\)
6- D
The trapezoid has one pair of parallel sides.
The second and third shape has perpendicular sides.
7- A
Add a number of all students to know the whole number of students.
\(86 + 32 =118\)
8- 8
\(40÷5 = 8\)
9- D
If \(1\) box has \(100\) flashcards so \(55\) boxes have \((55×100)\) \(5,500\) flashcards.
10- C
At a height of \(1\) centimeter, we have \(7\) pennies, so in height of \(4\) centimeters, we have \(7 × 4\) pennies.
Looking for the best resource to help you succeed on the 4th Grade FSA Math test?
The Best Books to Ace 4th Grade FSA Math Test
Related to This Article
More math articles
- Line Plot
- 4th Grade Common Core Math FREE Sample Practice Questions
- How to Compare and Order Rational Numbers?
- SSAT Upper Level Math FREE Sample Practice Questions
- How long is the SAT Test?
- A Comprehensive Collection of Free AFOQT Math Practice Tests
- 10 Most Common Pre-Algebra Math Questions
- The Ultimate 7th Grade TCAP Math Course (+FREE Worksheets)
- The Ultimate ISEE Upper Level Math Formula Cheat Sheet
- 3rd Grade MCA Math Worksheets: FREE & Printable
What people say about "10 Most Common 4th Grade FSA Math Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.