Subtracting Fractions with Unlike Denominators for 5th Grade

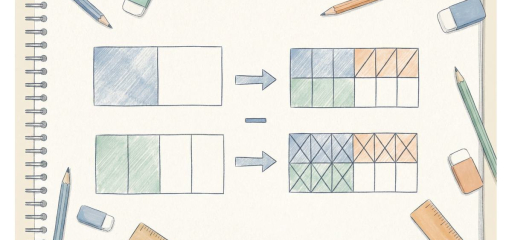
Subtracting fractions with unlike denominators requires finding a common denominator so we can subtract “like” parts—thirds from thirds, fourths from fourths. In Grade 5, students subtract fractions with different denominators by converting to equivalent fractions with a common denominator (usually the LCM of the denominators), then subtracting the numerators and keeping the denominator. This skill is used when finding differences in measurements, removing parts from wholes, and in real-world problems like “a rope was \(\frac{5}{6}\) meter and \(\frac{1}{4}\) meter was cut off.”

We cannot subtract \(\frac{3}{4} – \frac{1}{3}\) directly because fourths and thirds are different-sized parts. We need a common denominator. The LCM of 4 and 3 is 12. So \(\frac{3}{4} = \frac{9}{12}\) and \(\frac{1}{3} = \frac{4}{12}\). Now \(\frac{9}{12} – \frac{4}{12} = \frac{5}{12}\). The difference is \(\frac{5}{12}\).

DETAILED EXPLANATION

Steps to subtract fractions with unlike denominators:

1. Find the least common multiple (LCM) of the denominators—this will be the common denominator.

The Absolute Best Book to Ace Grade 5 Math

The Ultimate Elementary School Math Bundle Grade 3-5

Download

$109.99 Original price was: $109.99.$54.99Current price is: $54.99.

2. Convert each fraction to an equivalent fraction with that denominator.

3. Subtract the numerators; keep the denominator the same.

4. Simplify the result if possible.

If the first fraction is smaller than the second, we may need to borrow from the whole number part (when working with mixed numbers). For two proper fractions, we ensure the first is greater than or equal to the second; otherwise the difference would be negative (typically introduced in later grades).

Example: \(\frac{3}{4} – \frac{1}{3}\). LCM(4,3)=12. \(\frac{3}{4}=\frac{9}{12}\), \(\frac{1}{3}=\frac{4}{12}\). \(\frac{9}{12}-\frac{4}{12}=\frac{5}{12}\).

WORKED EXAMPLES WITH STEP BY STEP SOLUTIONS

Example 1

Subtract \(\frac{3}{4} – \frac{1}{3}\)

The Ultimate Middle School Math Bundle: Grades 6–8

Solutions:

Step 1: Denominators are 4 and 3. LCM of 4 and 3 is 12.

Step 2: Convert: \(\frac{3}{4} = \frac{3 \times 3}{4 \times 3} = \frac{9}{12}\); \(\frac{1}{3} = \frac{1 \times 4}{3 \times 4} = \frac{4}{12}\).

Step 3: Subtract numerators: \(\frac{9}{12} – \frac{4}{12} = \frac{5}{12}\).

Step 4: \(\frac{5}{12}\) is already in lowest terms.

Answer: \(\frac{5}{12}\)

Example 2

A rope was \(\frac{5}{6}\) meter. \(\frac{1}{4}\) meter was cut off. How much remains?

Solutions:

Mastering Grade 5 Math

Mastering Grade 5 Math The Ultimate Step by Step Guide to Acing 5th Grade Math

Download

$29.99 Original price was: $29.99.$16.99Current price is: $16.99.

Step 1: We need to subtract \(\frac{1}{4}\) from \(\frac{5}{6}\). LCM of 6 and 4 is 12.

Step 2: Convert: \(\frac{5}{6} = \frac{10}{12}\); \(\frac{1}{4} = \frac{3}{12}\).

Step 3: Subtract: \(\frac{10}{12} – \frac{3}{12} = \frac{7}{12}\).

Step 4: The rope that remains is \(\frac{7}{12}\) meter.

Answer: \(\frac{7}{12}\) meter

Example 3

Subtract \(\frac{2}{3} – \frac{2}{5}\)

Solutions:

Step 1: LCM of 3 and 5 is 15. Convert: \(\frac{2}{3} = \frac{10}{15}\); \(\frac{2}{5} = \frac{6}{15}\).

Step 2: Subtract: \(\frac{10}{15} – \frac{6}{15} = \frac{4}{15}\).

Step 3: \(\frac{4}{15}\) is in lowest terms.

Answer: \(\frac{4}{15}\)

Example 4

Subtract \(\frac{5}{6} – \frac{1}{2}\)

Solutions:

Step 1: LCM of 6 and 2 is 6. \(\frac{5}{6} = \frac{5}{6}\); \(\frac{1}{2} = \frac{3}{6}\).

Step 2: Subtract: \(\frac{5}{6} – \frac{3}{6} = \frac{2}{6}\).

Step 3: Simplify: \(\frac{2}{6} = \frac{1}{3}\).

Answer: \(\frac{1}{3}\)