Multiplying Fractions for 5th Grade: Numerators and Denominators

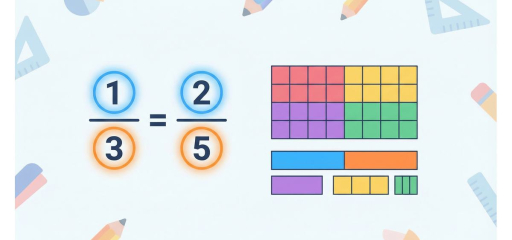
Multiplying fractions is used when finding parts of quantities—for example, “what is \(\frac{2}{3}\) of \(\frac{4}{5}\) cup?” or “what is \(\frac{1}{2}\) of a recipe that uses \(\frac{2}{3}\) cup flour?” In Grade 5, students multiply fractions by multiplying numerators and multiplying denominators, then simplifying if possible. The rule is simple: \(\frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\). This skill helps students scale recipes, find fractional parts of amounts, and solve real-world problems involving multiplication of parts.

Unlike addition and subtraction, we do NOT need a common denominator to multiply fractions. We simply multiply the numerators together and the denominators together. The result can often be simplified by finding the GCF of the numerator and denominator and dividing both. We can also simplify before multiplying by canceling common factors between numerators and denominators.

DETAILED EXPLANATION

Rule: \(\frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\).

Steps:

5 Full-Length Common Core Grade 5 Math Practice Tests: The Practice You Need to Ace the Common Core Math Test

$27.99 Original price was: $27.99.$17.99Current price is: $17.99.

The Absolute Best Book to Ace Grade 5 Math

The Ultimate Elementary School Math Bundle Grade 3-5

Download

$109.99 Original price was: $109.99.$54.99Current price is: $54.99.

1. Multiply numerators.

2. Multiply denominators.

3. Simplify the result (reduce to lowest terms).

Shortcut: Before multiplying, we can cancel any common factor between a numerator and a denominator. For example, \(\frac{3}{4} \times \frac{2}{9}\): the 3 and 9 share a factor of 3; the 2 and 4 share a factor of 2. Cancel: \(\frac{1}{4} \times \frac{2}{3} = \frac{2}{12} = \frac{1}{6}\).

WORKED EXAMPLES WITH STEP BY STEP SOLUTIONS

Example 1

Multiply \(\frac{2}{3} \times \frac{4}{5}\)

Solutions:

The Ultimate Middle School Math Bundle: Grades 6–8

Step 1: Multiply numerators: \(2 \times 4 = 8\).

Step 2: Multiply denominators: \(3 \times 5 = 15\).

Step 3: Product: \(\frac{8}{15}\).

Step 4: Check if \(\frac{8}{15}\) can be simplified. GCF(8, 15) = 1, so it is already in lowest terms.

Answer: \(\frac{8}{15}\)

Example 2

A recipe uses \(\frac{2}{3}\) cup flour. You make \(\frac{1}{2}\) of the recipe. How much flour?

Solutions:

Step 1: “Half of \(\frac{2}{3}\) cup” means multiply \(\frac{2}{3} \times \frac{1}{2}\).

Mastering Grade 5 Math

Mastering Grade 5 Math The Ultimate Step by Step Guide to Acing 5th Grade Math

Download

$29.99 Original price was: $29.99.$16.99Current price is: $16.99.

Step 2: Multiply numerators: \(2 \times 1 = 2\). Multiply denominators: \(3 \times 2 = 6\). Product: \(\frac{2}{6}\).

Step 3: Simplify: \(\frac{2}{6} = \frac{1}{3}\).

Step 4: You use \(\frac{1}{3}\) cup flour.

Answer: \(\frac{1}{3}\) cup

Example 3

\(\frac{3}{4} \times \frac{2}{9}\) = ?

Solutions:

Step 1: Multiply: \(3 \times 2 = 6\), \(4 \times 9 = 36\). Product: \(\frac{6}{36}\).

Step 2: Simplify: GCF(6, 36) = 6. \(\frac{6}{36} = \frac{1}{6}\).

Step 3: Alternatively, cancel before multiplying: 3 and 9 share factor 3; 2 and 4 share factor 2. \(\frac{1}{4} \times \frac{2}{3} = \frac{2}{12} = \frac{1}{6}\).

Answer: \(\frac{1}{6}\)

Example 4

Multiply \(\frac{5}{8} \times \frac{4}{15}\)

Solutions:

Step 1: Multiply: \(5 \times 4 = 20\), \(8 \times 15 = 120\). Product: \(\frac{20}{120}\).

Step 2: Simplify: GCF(20, 120) = 20. \(\frac{20}{120} = \frac{1}{6}\).

Answer: \(\frac{1}{6}\)

The Ultimate Middle School Math Bundle: Grades 6-8

$109.99 Original price was: $109.99.$54.99Current price is: $54.99.