Comparing and Ordering Fractions for 5th Grade: Unlike Denominators

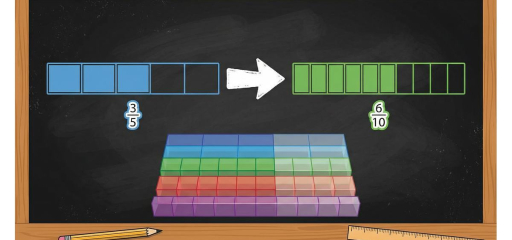
Comparing and ordering fractions helps students decide which fraction is larger, order fractions from least to greatest, and make sense of real-world situations like “who ate more pizza?” or “which measurement is longer?” In Grade 5, students compare fractions with unlike denominators by finding a common denominator (or a common numerator in some cases) or by converting to decimals. The key idea is that we can only compare fractions when they refer to the same whole and the same-size parts—so we need a common denominator to compare “apples to apples.”

To compare \(\frac{2}{3}\) and \(\frac{3}{4}\), we find a common denominator. The LCM of 3 and 4 is 12. \(\frac{2}{3} = \frac{8}{12}\) and \(\frac{3}{4} = \frac{9}{12}\). Since \(\frac{8}{12} < \frac{9}{12}\), we have \(\frac{2}{3} < \frac{3}{4}\). Alternatively, we could convert to decimals: \(\frac{2}{3} \approx 0.667\) and \(\frac{3}{4} = 0.75\), so \(\frac{3}{4}\) is greater.

DETAILED EXPLANATION

Methods to compare fractions:

1. Common denominator: Convert both fractions to equivalent fractions with the same denominator. The fraction with the larger numerator is greater.

The Absolute Best Book to Ace Grade 5 Math

The Ultimate Elementary School Math Bundle Grade 3-5

Download

$109.99 Original price was: $109.99.$54.99Current price is: $54.99.

2. Common numerator: In some cases, the fraction with the smaller denominator is greater (e.g., \(\frac{3}{4} > \frac{3}{5}\) because fourths are larger than fifths).

3. Cross-multiply: For \(\frac{a}{b}\) and \(\frac{c}{d}\), compare \(a \times d\) and \(b \times c\). If \(ad > bc\), then \(\frac{a}{b} > \frac{c}{d}\).

4. Decimal conversion: Convert both to decimals and compare.

To order fractions from least to greatest: Find a common denominator, convert all fractions, then order by numerator.

WORKED EXAMPLES WITH STEP BY STEP SOLUTIONS

Example 1

Which is greater: \(\frac{2}{3}\) or \(\frac{3}{4}\)?

Solutions:

The Ultimate Middle School Math Bundle: Grades 6–8

The Ultimate Middle School Math Bundle Grades 6-8

Download

$109.99 Original price was: $109.99.$54.99Current price is: $54.99.

Step 1: Find a common denominator. LCM of 3 and 4 is 12.

Step 2: Convert: \(\frac{2}{3} = \frac{2 \times 4}{3 \times 4} = \frac{8}{12}\); \(\frac{3}{4} = \frac{3 \times 3}{4 \times 3} = \frac{9}{12}\).

Step 3: Compare numerators: 8 < 9, so \(\frac{8}{12} < \frac{9}{12}\).

Step 4: Therefore \(\frac{2}{3} < \frac{3}{4}\). \(\frac{3}{4}\) is greater.

Answer: \(\frac{3}{4}\) is greater.

Example 2

Order from least to greatest: \(\frac{1}{2}\), \(\frac{2}{5}\), \(\frac{3}{10}\)

Solutions:

Step 1: LCM of 2, 5, 10 = 10. Convert: \(\frac{1}{2} = \frac{5}{10}\); \(\frac{2}{5} = \frac{4}{10}\); \(\frac{3}{10} = \frac{3}{10}\).

Mastering Grade 5 Math

Mastering Grade 5 Math The Ultimate Step by Step Guide to Acing 5th Grade Math

Download

$29.99 Original price was: $29.99.$16.99Current price is: $16.99.

Step 2: Order by numerator: \(\frac{3}{10} < \frac{4}{10} < \frac{5}{10}\).

Step 3: In original form: \(\frac{3}{10}\), \(\frac{2}{5}\), \(\frac{1}{2}\).

Answer: \(\frac{3}{10}\), \(\frac{2}{5}\), \(\frac{1}{2}\)

Example 3

Sam ate \(\frac{2}{5}\) of a pizza and Mia ate \(\frac{1}{2}\). Who ate more?

Solutions:

Step 1: Compare \(\frac{2}{5}\) and \(\frac{1}{2}\). Common denominator: 10. \(\frac{2}{5} = \frac{4}{10}\); \(\frac{1}{2} = \frac{5}{10}\).

Step 2: \(\frac{5}{10} > \frac{4}{10}\), so \(\frac{1}{2} > \frac{2}{5}\).

Step 3: Mia ate more.

Answer: Mia ate more.

Example 4

Which is greater: \(\frac{4}{7}\) or \(\frac{5}{9}\)?

Solutions:

Step 1: Common denominator: LCM of 7 and 9 = 63. \(\frac{4}{7} = \frac{36}{63}\); \(\frac{5}{9} = \frac{35}{63}\).

Step 2: 36 > 35, so \(\frac{36}{63} > \frac{35}{63}\).

Answer: \(\frac{4}{7}\) is greater.